SPE MATH congruences
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
martyy
- Messages: 7
- Enregistré le: 02 Nov 2009, 22:37
-
 par martyy » 02 Nov 2009, 22:55
par martyy » 02 Nov 2009, 22:55
Bonjour a tous je suis un élève de terminale S spécialité mathématique
j'ai un DM très important a rendre bien en spé math qui est assez dure
il est composé de 2 exo j'ai réussi le premier car il était assez détaillé et donc j'était plus guidé,
mais le deuxiéme est très court et je ne sais pas par ou commencer...
l'énoncé est : prouver que pour tout n entier naturel avec n

2

"congrue à" 0 [11] (modulo 11)
voila... j'espére que vous pourrez m'aider
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Nov 2009, 23:29
par Nightmare » 02 Nov 2009, 23:29
Salut !
On travaille modulo 11, c'est à dire qu'on considère que tous les entiers qui ont le même reste modulo 11 sont égaux, ainsi on ne travaille plus qu'avec les 11 premiers "nombres" (qui ne sont pas réellement des nombres mais des
classes de nombre).
L'idée alors est de "réduire" notre expression modulo 11. Par exemple prenons
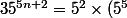^{n})
Modulo 11, on a

car

donc le reste est 3. On a aussi

(toujours modulo 11)
Au final,

Essaye de faire pareil pour les autre et voir pourquoi la somme vaut 0.
:happy3:
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 02 Nov 2009, 23:46
par zerkel » 02 Nov 2009, 23:46
bonsoir, ne serait-ce pas plutôt un "-"7 ? (sinon je suis absolument d'accord avec nightmare)
-
zerkel
- Membre Relatif
- Messages: 134
- Enregistré le: 01 Nov 2009, 18:08
-
 par zerkel » 02 Nov 2009, 23:57
par zerkel » 02 Nov 2009, 23:57
euh en fait nightmare t'as fait une petite faute :$ (peut être volontaire)

.
Par contre bien sûr la méthode est bonne probablement juste une faute de frappe
Et sinon dans l'énoncé du problème c'est un "-"7, car autrement on trouve que le tout est congru à 3 modulo 11.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Nov 2009, 00:22
par Nightmare » 03 Nov 2009, 00:22
Salut !
Oui je ne sais pas pourquoi mon 5 c'est subitement transformé en 1, merci pour la correction :happy3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 08:33
par benekire2 » 03 Nov 2009, 08:33
Pour le

je te propose d'étudier
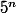
,
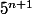
etc.. de manière à ce que tu puisse arriver a voir de quoi ce raproche le 5n-1
-
martyy
- Messages: 7
- Enregistré le: 02 Nov 2009, 22:37
-
 par martyy » 03 Nov 2009, 09:28
par martyy » 03 Nov 2009, 09:28
toutes mes excuses c'est effectivement -7
:s je travail sans l'énoncé tellement je me suis cassé la téte dessus merci a tous
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 09:40
par benekire2 » 03 Nov 2009, 09:40
Alors c'est bon ? Problème résolu ??
-
martyy
- Messages: 7
- Enregistré le: 02 Nov 2009, 22:37
-
 par martyy » 03 Nov 2009, 10:03
par martyy » 03 Nov 2009, 10:03
la méthode m'aide beaucoup merci pour le

j'ai parfaitement compris je crois , au final on a

=3[11]
et le 7 c'est pas trop dur ^^
pour le

je procède ainsi: je pose
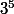
=243 or 243=1[11]
donc
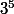
= 1[11]

=1[11] car ici n supérieur ou égal a 2
et 7=-4[11]
au final quand j'aditionne tout cela me donne 1+3-4=0
merci a tous! en plus d'avoir bien fait mon exo sa m'aide pour la méthode merci a tous!
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Nov 2009, 10:17
par benekire2 » 03 Nov 2009, 10:17
C'est le but, les méthodes c'est le principal, l'exo en lui même ne sert qu'a acquérir une méthode, rien de plus ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 181 invités
