Congruences TS Spé Math ..
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 15:00
par Sapphire » 19 Nov 2006, 15:00
Bonjour,
J'ai un petit problème dans la résolution de cet exercice :
Résoudre dans Z : 3x² + 4x "congru à" 0 (mod. 21)
J'ai essayé de résoudre ça mais je tombe systématiquement sur x congru à 3 mod 21 .. Si quelqu'un pouvait maider, ce serait tres utile .
Merci
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 15:07
par zebdebda » 19 Nov 2006, 15:07
Posons X = 3x²+4x. La décomposition en facteurs premiers de 21 est 3x7 donc :

équivaut à

et

-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 15:08
par Sapphire » 19 Nov 2006, 15:08
Je réfléchis à ça et je reviens :happy2:
Merci
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 16:03
par Sapphire » 19 Nov 2006, 16:03
:mur: Je n'y arrive toujours pas :triste:
Je crois que je n'ai rien compris au cours des congruences ..
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 16:07
par zebdebda » 19 Nov 2006, 16:07
Je vais t'aider. Je crains de ne pas utiliser la méthode la plus pratique, car je n'ai pas fait de congruence depuis longtemps, mais c'est toujours mieux que rien !
Tu dois donc chercher x tel que

et

Prenons la première, c'est la plus facile.

cela se simplifie très vite : qu'obtiens tu ?
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 16:26
par Sapphire » 19 Nov 2006, 16:26
Jobtiens 4x congru à 0 [3] parce que 3 congru à 0 [3] .
Mais 4 est congru à 1 [3], dc on a directement x congru à 0 [3] non ?
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 16:29
par zebdebda » 19 Nov 2006, 16:29
et
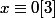
car

.
ça c'est fait !
Au tour de la deuxième maintenant.

Je te propose de factoriser.
Comme 7 est premier, le produit de facteurs sera congru à 0 modulo 7 si l'un des facteurs est congru à 0 modulo 7.
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 16:34
par Sapphire » 19 Nov 2006, 16:34
Dc on a soit x congru a 0 [7], soit 3x+4 congru à 0 [7].
J'imagine que c'est la premiere qui est bonne, et on aura :
x congru a 0 [7] et [3]. La solution serait alors x congru à 0 [21] parce 21 = 3 x 7 nan ?
Mais comment montrer que 3x + 4 congru à 0 [7] n'est pas la bonne ? ...
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 16:38
par zebdebda » 19 Nov 2006, 16:38
Il n'y en a pas une bonne et une fausse : les deux possiblités fonctionnent. (c'est une équation de degré 2 donc plusieurs solutions)
il faut maintenant se débrouiller avec le

Pour celle-ci un indice :

-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 16:49
par Sapphire » 19 Nov 2006, 16:49
Ui c'est vrai j'ai un peu honte de ce que j'ai dit :hum:
Dc apres reflexion : 3x+4 congru à 0 [7] équivaut à : 3x-3 congru à 0 [7],
soit 3(x-1) congru à 0 [7],
soit x-1 congru à 0 [7],
soit x congru à 1 [7]
C'est ce qu'il fallait trouver ?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 19 Nov 2006, 16:51
par BancH » 19 Nov 2006, 16:51
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 16:54
par Sapphire » 19 Nov 2006, 16:54
Je ne pense pas que ce soit ça qui me soit demandé..
Je crois plutôt qu'il faut que je travaille avec les congruences, comme le fait zebdebda ..
Merci quand même BancH de ton aide :)
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 17:00
par zebdebda » 19 Nov 2006, 17:00
Je suis d'accord avec ta solution :

équivaut à
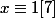
Maintenant le travail n'est pas fini.
Il faut trouver tous les entiers congru à la fois à 0 modulo 3 et à 1 modulo 7.
ça normalement tu sais faire.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 19 Nov 2006, 17:12
par BancH » 19 Nov 2006, 17:12
Avec les congru il faut faire:
Si
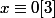
alors

Si

alors

Si

alors

Si
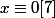
alors

Si
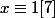
alors

Si

alors

Si

alors

Si

alors

Si

alors

Si

alors

Donc les solutions sont toutes des multiples de

.
La moitié sont multiples de

, et les autres sont congrues à

modulo

.

et


et

Or, si

est solution, alors

est solution.
Donc
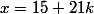
ou
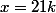
avec

entier relatif.
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 17:15
par Sapphire » 19 Nov 2006, 17:15
Avec ces solutions, on a :x congru à 1 [7], soit x = 7k+1, k appartenant à Z
et x congru à 0 [3], soit x = 3k'+1, k' appartenant à Z.
Mais après je ne sais pas vraiment ce qu'il faut faire ..
J'ai pas vraiment compris le cours sur la congruence :triste:
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 17:19
par zebdebda » 19 Nov 2006, 17:19
en fait tu as x=7k+1=3k'
Tu cherches maintenant k et k'
Cela revient à 7k-3k'=1
Si on les appelle u et v ça te dira sans doute quelque chose : 7u-3v=1 ?
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 17:19
par Sapphire » 19 Nov 2006, 17:19
Merci BancH de ta réponse, mais je préfère finir ce que j'ai commencé !
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 17:21
par Sapphire » 19 Nov 2006, 17:21
Le u et et le v me rappellent les suites de Première, mais je doute que ce soit ça que tu attendais :hein:
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 19 Nov 2006, 17:30
par zebdebda » 19 Nov 2006, 17:30
Non pas du tout ! c'est une équation de Bezout. Généralement on fait ça avant les congruences
-
Sapphire
- Membre Naturel
- Messages: 83
- Enregistré le: 19 Nov 2006, 14:57
-
 par Sapphire » 19 Nov 2006, 17:32
par Sapphire » 19 Nov 2006, 17:32
Alors là ... Je suis l'excpetion ^^
C'est le premier chapitre que l'on fait en Spé et on a pas vu ce théorème ...
Mais je me souviens d'en avoir parlé l'année dernière avec des amis et il y a une histoire de nombres premiers entre eux non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
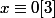 alors
alors 
 alors
alors 
 alors
alors 
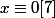 alors
alors 
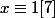 alors
alors 
 alors
alors 
 alors
alors 
 alors
alors 
 alors
alors 
 alors
alors 
 .
. , et les autres sont congrues à
, et les autres sont congrues à  modulo
modulo  .
. et
et 
 et
et 
 est solution, alors
est solution, alors  est solution.
est solution.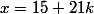 ou
ou 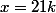 avec
avec  entier relatif.
entier relatif.