Sommes d'entiers consécutifs élevés à une même puissance
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Aoû 2010, 14:05
par Dinozzo13 » 23 Aoû 2010, 14:05
Salut !
Sachant que :
}{2})
(2n+1)}{6})
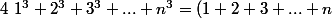^2=\frac{n^2(n+1)^2}{4})
(n entier naturel non nul)
Peut-on, à partir de ces résultats exprimer de la même manière :

?
Et pourquoi pas généraliser, si

:

?
-
Anonyme
 par Anonyme » 23 Aoû 2010, 14:16
par Anonyme » 23 Aoû 2010, 14:16
Il y a quelques semaines j'ai essayer de chercher une generalisation mais j'ai pas trouver. Mais si j'ai les formules des n-1 premieres puissance je sais retrouver la n ieme.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Aoû 2010, 14:19
par Dinozzo13 » 23 Aoû 2010, 14:19
J'étais sûr que tu viendrais ^^
Ah, t'as pas trouvé :hum:
T'as trouvé déjà quelque chose pour :

?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Aoû 2010, 14:19
par Nightmare » 23 Aoû 2010, 14:19
Salut,
Soit
=\Bigsum_{k\le n} k^{p})
Je vous laisse le soin de montrer que
=\Bigsum_{k=0}^{p+1} C_{p+1}^{k} \sigma_{x}(n))
, puis en déduire que
^{p+1}=\Bigsum_{k\le p} C_{p+1}^{k} \sigma_{x}(n))
, ce qui permet d'avoir chaque somme de puissances par rapport aux sommes des puissances précédentes.
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 23 Aoû 2010, 14:24
par Djmaxgamer » 23 Aoû 2010, 14:24
Dinozzo13 a écrit:Salut !
Sachant que :
}{2})
(2n+1)}{6})
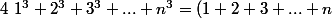^2=\frac{n^2(n+1)^2}{4})
(n entier naturel non nul)
Peut-on, à partir de ces résultats exprimer de la même manière :

?
Et pourquoi pas généraliser, si

:

?
Oui on peut le faire : je me souviens avoir fait un DM où l'une des conclusions était cette généralisation. Si je le retrouve je t'en ferais part.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 23 Aoû 2010, 14:27
par Zweig » 23 Aoû 2010, 14:27
C'est possible, faut aller voir du côté des nombres de Bernoulli.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 23 Aoû 2010, 14:50
par Olympus » 23 Aoû 2010, 14:50
Si je ne m'abuse pas, pour
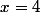
, il suffit de regarder la différence
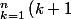^5 - \bigsum^{n}_{k=1} k^5)
.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 23 Aoû 2010, 16:59
par Dinozzo13 » 23 Aoû 2010, 16:59
Ah ouais :ptdr:
j'me rappelais même plus que je l'avais fait ^^
Merci beaucoup ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
?
:
?