Sommes des carrés... Suites numériques.
13 messages
- Page 1 sur 1
Sommes des carrés... Suites numériques.
Bonjour, je bloque sur ce problème...
Soit (Un) la suite définie pour tout entier naturel n non nul par :
Un=
n
;)k²
k=1
1) Donner l'expression de Un+1 en fonction de Un et le premier terme U1 de la suite.
2) On considère maintenant la suite (Wn) définie par :
Wn = (n(n+1))(2n+1)/6
Déterminer W1 et Wn+1-Wn, puis l'expression de Wn+1 en fonction de Wn
3) En déduire que
n
;)k² = (n(n+1))(2n+1)/6
k=1
PISTE : Si deux suites ont le même premier terme et si, pour les deux suites, chaque terme se déduit du précédent par la même relation, alors ces suites sont égales.
En fait je me doute qu'il va falloir utiliser la propriété donnée qui s'appliquera pour (Wn) et pour (Un)... mais je bloque dès la question 1, quand ils demandent de donner l'expression de Un+1 en fonction de Un : j'ai aucune idée de ce qu'il faut faire pour ça.
Soit (Un) la suite définie pour tout entier naturel n non nul par :
Un=
n
;)k²
k=1
1) Donner l'expression de Un+1 en fonction de Un et le premier terme U1 de la suite.
2) On considère maintenant la suite (Wn) définie par :
Wn = (n(n+1))(2n+1)/6
Déterminer W1 et Wn+1-Wn, puis l'expression de Wn+1 en fonction de Wn
3) En déduire que
n
;)k² = (n(n+1))(2n+1)/6
k=1
PISTE : Si deux suites ont le même premier terme et si, pour les deux suites, chaque terme se déduit du précédent par la même relation, alors ces suites sont égales.
En fait je me doute qu'il va falloir utiliser la propriété donnée qui s'appliquera pour (Wn) et pour (Un)... mais je bloque dès la question 1, quand ils demandent de donner l'expression de Un+1 en fonction de Un : j'ai aucune idée de ce qu'il faut faire pour ça.
Salut !
Ca va peut-être te sembler bête, mais, pour pouvoir exprimer en fonction de
en fonction de  , encore faut-il calculer
, encore faut-il calculer  :++:
:++:
Une fois cela fait, tu peut en déduire en fonction de
en fonction de  assez facilement.
assez facilement.
( est une somme de
est une somme de  terme et
terme et  est la somme de
est la somme de  dont
dont  de ces termes sont exactement les même que dans
de ces termes sont exactement les même que dans  ).
).
Enfin pour calculer , calcule
, calcule 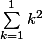 .
.
Tu viens définir ta suite) à l'aide d'une relation de récurrence et de son terme initial :
à l'aide d'une relation de récurrence et de son terme initial :
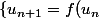 \\ u_1 = ...) .
.
:+++:
Ca va peut-être te sembler bête, mais, pour pouvoir exprimer
Une fois cela fait, tu peut en déduire
(
Enfin pour calculer
Tu viens définir ta suite
:+++:
Dinozzo13 a écrit:Salut !
Ca va peut-être te sembler bête, mais, pour pouvoir exprimeren fonction de
, encore faut-il calculer
:++:
Une fois cela fait, tu peut en déduireen fonction de
assez facilement.
(est une somme de
terme et
est la somme de
dont
de ces termes sont exactement les même que dans
).
Enfin pour calculer, calcule
.
Tu viens définir ta suiteà l'aide d'une relation de récurrence et de son terme initial :
.
:+++:
Okidoki merci beaucoup :we:
Bon alors j'ai cherché et en gros et trouvé :
Un=n²
Un+1= (n+1)²
U1= 1
Mais même quand j'ai Un+1 je vois pas comment on peut en déduire Un+1 en fonction de Un... Je connais pas la méthode. Désolé hein, :lol3:
Je suis un monstre  Mais c'est bien fait vu que j'aime pas les 1. :bad3:
Mais c'est bien fait vu que j'aime pas les 1. :bad3:
Alors on a Un+1= Un +(n+1)² et U1= 1
Pour la 2) donc... W1= 1
Wn+1-Wn=((n+1)(n+2)(2n+3)-n(n+1)(2n+1))/6=(6n²+12n+6)/6=(n+1)²
Ainsi, Wn+1=Wn+(n+1)²
Et donc pour la 3), on se sert de la propriété donnée pour donc dire que :
n
;)k²= n(n+1)(2n+1)/6
k=1
Bon bah voila voila.. :zen: Merci à tous ! My life is saved !
Alors on a Un+1= Un +(n+1)² et U1= 1
Pour la 2) donc... W1= 1
Wn+1-Wn=((n+1)(n+2)(2n+3)-n(n+1)(2n+1))/6=(6n²+12n+6)/6=(n+1)²
Ainsi, Wn+1=Wn+(n+1)²
Et donc pour la 3), on se sert de la propriété donnée pour donc dire que :
n
;)k²= n(n+1)(2n+1)/6
k=1
Bon bah voila voila.. :zen: Merci à tous ! My life is saved !
Vlarck ! a écrit:Je suis un monstreMais c'est bien fait vu que j'aime pas les 1. :bad3:
Alors on a Un+1= Un +(n+1)² et U1= 1
Pour la 2) donc... W1= 1
Wn+1-Wn=((n+1)(n+2)(2n+3)-n(n+1)(2n+1))/6=(6n²+12n+6)/6=(n+1)²
Ainsi, Wn+1=Wn+(n+1)²
Et donc pour la 3), on se sert de la propriété donnée pour donc dire que :
n
;)k²= n(n+1)(2n+1)/6
k=1
Bon bah voila voila.. :zen: Merci à tous ! My life is saved !
Yeah ! :++:
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
