Solution d'équation encadrement
27 messages
- Page 1 sur 2 - 1, 2
solution d'équation encadrement
merci d'avance pour votre aide:
verifier que l'équation 3x^4+4x³-12x²+5=0 admet une unique solution x0 dans l'intervalle [-1,0] donner un encadrement d'amplitude 10^-² de xo a l'aide de la calculatrice.
verifier que l'équation 3x^4+4x³-12x²+5=0 admet une unique solution x0 dans l'intervalle [-1,0] donner un encadrement d'amplitude 10^-² de xo a l'aide de la calculatrice.
Bonjour,
posons=3x^4+4x^3-12x^2+5) . On veut montrer que f s'annule une et une seule fois sur l'intervalle [-1,0]. Il suffit d'étudier f sur cet intervalle et d'utiliser le théorème de la bijection. Pour l'utiliser, il faut vérifier ses hypothèses, à savoir que f est :
. On veut montrer que f s'annule une et une seule fois sur l'intervalle [-1,0]. Il suffit d'étudier f sur cet intervalle et d'utiliser le théorème de la bijection. Pour l'utiliser, il faut vérifier ses hypothèses, à savoir que f est :
posons
- continue sur [-1,0],
- strictement monotone sur [-1,0],
- f(-1) et f(0) sont de signe oppposé.
solution d'équation encadrement
f est derivable sur [-1,0]
f est strictement croissante sur [-1,0] ( dapré le tablo de variation)
0 est compris entre f(-1) et f(0)
donc l'équation 3x^4+4x³-12x²+5=0 admet une unique solution xo dans [-1,0]
f est strictement croissante sur [-1,0] ( dapré le tablo de variation)
0 est compris entre f(-1) et f(0)
donc l'équation 3x^4+4x³-12x²+5=0 admet une unique solution xo dans [-1,0]
La dérivabilité n'est pas nécessaire. Le théorème des valeurs intermédiaires ne demande que la continuité. Cependant, la dérivabilité est suffisante car "dérivable implique continue" (phrase à connaître par coeur). Par ailleurs, quand on utilise un théorème, il faut l'énoncer !
Je dirais donc :
et ce sera parfait ! :we:
Je dirais donc :
marocain94 a écrit:f est derivable sur [-1,0] donc f est continue sur [-1,0]
f est strictement croissante sur [-1,0] ( d'après le tableau de variations :happy3: )
0 est compris entre f(-1) et f(0)
donc d'après le théorème de la bijection l'équation f(x)=0 c'est-à-dire 3x^4+4x³-12x²+5=0 admet une unique solution xo dans [-1,0]
et ce sera parfait ! :we:
Re : solution d'équation encadrement
a ok merci, et aprés pour lencadrement avec la calculatrice je sait qu'il faut utliser le tableur mais je ne sait pa comment
On rentre l'équation de la onction, on règle le pas du tableur sur 0,1 et on regarde à partir de -1.
On a donc :
-1 | f(-1)
-0,9 | f(-0,9)
-0,8 | f(-0,8)
-0,1 | f(-0,1)
0 | f(0)
On regarde entre quels nombres ça change de signe. Ca donne un encadrement à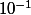 près.
près.
On se place dans ce nouvel intervalle et on règle le pas sur 0,01. On cherche à nouveau quand ça change de signe et ça donne un encadrement de à
à 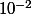 près.
près.
On a donc :
-1 | f(-1)
-0,9 | f(-0,9)
-0,8 | f(-0,8)
-0,1 | f(-0,1)
0 | f(0)
On regarde entre quels nombres ça change de signe. Ca donne un encadrement à
On se place dans ce nouvel intervalle et on règle le pas sur 0,01. On cherche à nouveau quand ça change de signe et ça donne un encadrement de
Re : solution d'équation encadrement
j'ai taper a la calculatrice tout sa, et je vois a x=-0.62 y=-0.12 et a x=-0.61 y=0.042 c'est bien sa ?
Re : solution d'équation encadrement
donc l'équation admet une unique solution xo dans [-1,0] :
-0.7
f(-0.61)= 0.4225123 > 0
f(-0.62)= -0.12282192 < 0
-0.7
f(-0.61)= 0.4225123 > 0
f(-0.62)= -0.12282192 < 0
Re : solution d'équation encadrement
euh oui erreur béte j'ai inverser comme j'ai taper sa trop vite c'est -0.62
Re : solution d'équation encadrement
Merci pour ton aide, j'ai une autre question si sa ne te dérange pas pour le meme exercice , apré avoir étudier le sens de variations de la fonction
f(x)= 3x^4+4x^3-12x²+5 , on me demande de construire C apré avoir determiné les coordonnées de quelques points; et d'utiliser la courbe pour donner le nombre de solutions de chacune des équations suivantes : 3x^4+4x^3-12x²+5 =10 ;
3x^4+4x^3-12x²+5 =-18 ; 3x^4+4x^3-12x²+5 =50.
j'ai construit C grace au tableau de variations et de signes mais aprés je suis bloquer
f(x)= 3x^4+4x^3-12x²+5 , on me demande de construire C apré avoir determiné les coordonnées de quelques points; et d'utiliser la courbe pour donner le nombre de solutions de chacune des équations suivantes : 3x^4+4x^3-12x²+5 =10 ;
3x^4+4x^3-12x²+5 =-18 ; 3x^4+4x^3-12x²+5 =50.
j'ai construit C grace au tableau de variations et de signes mais aprés je suis bloquer
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
