Similitudes

[parsy]

Bonjour, je suis actuellement en TS et je n'arrive pas à résoudre ce problème, est-ce que quelqu'un peut m'aider? Merci d'avance.


Le plan est muni d'un repère orthonormal direct (O;u,v) (Unité graphique 1 cm)

1) On note A,B et C les points d'affixes respectives:
2i; -1+4i et 5+2i

On note t la translation de vecteur BC, S la symétrie d'axe (AB) et on pose f= t°S.
On désigne par A' et B' respectivement les images de A et B par f.
Calculer les affixes de A' et B'.

2) Démontrer que f est une similitude indirecte.
Quel est son rapport?

3) Démontrer que l'écriture complexe de f est:
z'=1/5(-3-4i)z+1/5(38-6i) (z avec une barre dessus)

4) Déterminer l'ensemble des points invariants par f.
f est-elle une symétrie orthogonale?

5) Soit D le point d'affixe 3+6i, delta la médiatrice de [BD] et S' la symétrie d'axe delta.
a) Démontrer que les droites delta et (AB) sont parallèles.
Déterminer S°S'.

b) Montrer que f°S' est la translation notée t' de vecteur DC.
En déduire que f=t'°S'.


Merci beaucoup de m'aider, je bloque dés la première question

[becirj]

Bonjour

) On note A,B et C les points d'affixes respectives:
2i; -1+4i et 5+2i

On note t la translation de vecteur BC, S la symétrie d'axe (AB) et on pose f= t°S.
On désigne par A' et B' respectivement les images de A et B par f.
Calculer les affixes de A' et B'.

La première application est S. Par la symétrie S, S(A)=A et S(B)=B.
Le vecteur de la translation a pour affixe 5+2i)-(-1+4i)=6-2i.
L'image de A par t est le point A ' tel que donc ,

Le vecteur de la translation étant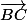 , t(B)=C.

f(A)=A ' d'affixe 6 et f(B)=B'=C d'affixe 5+2i.

2) Démontrer que f est une similitude indirecte.
Quel est son rapport?

Une translation est une similitude directe de rapport 1 et une symétrie axiale est une similitude indirecte de rapport (-1) donc f est une similtude indirecte de rapport (-1)x1=(-1)

Je te laisse continuer un peu.

[parsy]

Merci j'ai compris la première partie, mais la suite non, aidez moi s'il vous plait.

[becirj]

3) Démontrer que l'écriture complexe de f est:
z'=1/5(-3-4i)z+1/5(38-6i) (z avec une barre dessus)

Il faut commencer par déterminer l'écriture complexe de S. L'écriture complexe d'une similitude indirecte est de la forme a et b étant des complexes.
A et B sont leurs propres images donc on peut remplacer par le conjugué de l'affixe de A et on a aussi z'=affixe de A et même chose pour B. On obtient le système :


Je te laisse résoudre le système pour trouver a et b . On obtient :


D'autre part t a pour expression complexe :

Soit M un point d'affixe z, M' d'affixe z' son image par S et M" d'affixe z" l'image de M' par t. Il faut déterminer z" en fonction de z.
z"=z'+6+2i et on remplace z' par son expression :


On a ainsi obtenu l'expression complexe de f. J'ai détaillé pour que tu vois bien la méthode et on peut remplacer sans problème z" par z'.

4) Déterminer l'ensemble des points invariants par f.
f est-elle une symétrie orthogonale?

Un point invariant est un point qui est égal à son image donc il faut résoudre l'équation z"=z soit

Comme l'équation comporte à la fois z et son conjugué, on passe par la forme algébrique de z : x+yi et on écrit que les parties réelles et imaginaires des 2 membres de l'équation doivent être respectivement égales ce qui conduit à un système de 2 équations à 2 inconnues x et y

Je te laisse faire le calcul, tu devrais obtenir que le système n'a pas de solution;
f n'a pas de point invariant, ce n'est donc pas une symétrie orthogonale qui elle possèderait une droite de points invariants.

5) Soit D le point d'affixe 3+6i, delta la médiatrice de [BD] et S' la symétrie d'axe delta.
a) Démontrer que les droites delta et (AB) sont parallèles.

Il suffit de montrer que les vecteurs sont orthogonaux.

Déterminer S°S'.

Si tu as vu dans le cours que la composée de 2 symétries orthogonales d'axes parallèles est une translation , tu appliques le cours et tu détermines le vecteur de la translation.

Sinon tu commences par déterminer l'écriture complexe de S' en utilisant par exemple que S'(B)=D et, en appelant E, le milieu de [BD], S'(E)=E.

Puis tu détermines de la même manière que l'on détermine f.

On obtient

b) Montrer que f°S' est la translation notée t' de vecteur DC.
En déduire que f=t'°S'.

On peut faire cette question sans calcul.

car la composition des similitudes est associative.
En utilisant le résultat de la question précédente on obtient :



Si on compose à droite avec S', on obtient :
Or est l'identité du plan donc soit

[parsy]

Merci beaucoup, je vais essayé de comprendre tout ça.

[parsy]

Bonsoir Becirj, il se trouve que je n'arrive pas à résoudre le systéme de la question 3 pour trouver a et b, pouvez-vous m'aider merci.

[becirj]

Bonsoir

Le système équivaut à :


Je transforme la deuxième équation :