Signification de la phrase "Soit x appartient à E"
69 messages
- Page 1 sur 4 - 1, 2, 3, 4
signification de la phrase "Soit x appartient à E"
Bonjour,
Svp,quelle est la signification de la phrase "Soit x appartient à E",qu'on écrit dans la plupart du temps dans notre démonstration lorsqu'il s'agit d'une assertion de type "\forall x \in E ;\boldsymbol{A(x)}"
Svp,quelle est la signification de la phrase "Soit x appartient à E",qu'on écrit dans la plupart du temps dans notre démonstration lorsqu'il s'agit d'une assertion de type "\forall x \in E ;\boldsymbol{A(x)}"
Re: signification de la phrase "Soit x appartient à E"
La phrase se lit en réalité : Soit x appartenant à E
Ca peut être aussi : Soit x un entier pair ; Soit x un réel
Revenons à ton cas : Soit x appartenant à E
On a un ensemble E qui a été défini.
Par exemple, E , ça peut être l'ensemble des élèves de ton lycée.
Soit x appartenant à E , ça veut dire : prenons un élève au hasard.
Et derrière , on va dire : x a forcément telle propriété.
Soit E l'ensemble des élèves de mon lycée.
Soit x un élément de E.
Alors x a forcément entre 14 et 21 ans.
La propriété 'avoir entre 14 et 21 ans' est VRAIE pour tous les élèves du lycée.
Ca peut être aussi : Soit x un entier pair ; Soit x un réel
Revenons à ton cas : Soit x appartenant à E
On a un ensemble E qui a été défini.
Par exemple, E , ça peut être l'ensemble des élèves de ton lycée.
Soit x appartenant à E , ça veut dire : prenons un élève au hasard.
Et derrière , on va dire : x a forcément telle propriété.
Soit E l'ensemble des élèves de mon lycée.
Soit x un élément de E.
Alors x a forcément entre 14 et 21 ans.
La propriété 'avoir entre 14 et 21 ans' est VRAIE pour tous les élèves du lycée.
Re: signification de la phrase "Soit x appartient à E"
YasserKabiri a écrit: "\forall x \in E ;\boldsymbol{A(x)}"
Après mise en tex, voici ce que cela donne (après sélection du texte et clic sur le bouton "tex")
En général quand on dit "soit x un élément de E", on veut effectivement dire que x est un élément quelconque de E. En s'arrêtant sur ce point cela indique bien
Exemple, "soit x un nombre réel ; alors son carré est positif" cela s'écrit bel et bien
Quand cela apparaît dans le cadre d'une démonstration, c'est aussi ce qu'on veut dire : par exemple, quand on veut démontrer une limite particulière, on peut écrire en plein milieu de la démonstration "soit
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: signification de la phrase "Soit x appartient à E"
Salut hdci,
comment explique-t-on à un collégien voire lycéen la notation:
Pour tout k entier, si k multiple de 6 alors k pair
Si l'élève fait une disjonction de cas,
1) k multiple de 6
2) k impair
3) k pair non multiple de 6
Comment l'élève s'en sort pour faire la cas , k impair ?
k impair, si k multiple de 6 ce la donne quoi chez un collégien et à partir de quelle classe lycée cela ne pose plus problème?
comment explique-t-on à un collégien voire lycéen la notation:
Pour tout k entier, si k multiple de 6 alors k pair
Si l'élève fait une disjonction de cas,
1) k multiple de 6
2) k impair
3) k pair non multiple de 6
Comment l'élève s'en sort pour faire la cas , k impair ?
k impair, si k multiple de 6 ce la donne quoi chez un collégien et à partir de quelle classe lycée cela ne pose plus problème?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
Bonjour Beagle,
Dans le cas que tu cites, la disjonction de k (que ferait l'élève) est incorrecte. Puisque c'est "pour tout k, si k multiple de 6 alors k est pair", je présenterais les choses ainsi :
Je n'enseigne pas au collège ; mais je pense qu'à ce niveau (collégien), je dirai qu'on ne considère que la situation où l'hypothèse "si..." est vérifiée, car les autres n'ont pas d'objet. Je monterai également avec deux exemples que dans le cas où l'hypothèse n'est pas vérifiée, la conclusion n'est pas garantie (prendre k=3 et k=4).
A partir de la seconde, je commence à indiquer qu'une proposition de type "si H alors C" est vraie quand l'hypothèse H est fausse. pour faire "comprendre" cela je prend souvent des exemples tirés de la vie de tous les jours, par exemple en utilisant un argument de type "absurde" comme "c'est ça et moi je suis le pape", qui est un argument utilisé pour indiquer à son interlocuteur qu'on ne croit pas ce qu'il dit ("si ce que tu dis est vrai, alors je suis le pape" ; ceci pour arriver au fait qu'en mathématiques "Si H alors C" est vraie quand H est fausse.
En terminale (spécialité maths), je fais les tables de vérité.
Cela répond-il à ta question ?
Dans le cas que tu cites, la disjonction de k (que ferait l'élève) est incorrecte. Puisque c'est "pour tout k, si k multiple de 6 alors k est pair", je présenterais les choses ainsi :
- puisque l'hypothèse est "si k est multiple de 6", on ne considère que ce cas-là (démonstration directe).
- si on veut vraiment faire une disjonction de cas, il faut bien déterminer à quel moment. La disjonction de cas peut en effet porter sur le "pour tout k", ou bien pour le "k est multiple de 6".
- Si elle porte sur le "pour tout k", il n'y a que deux cas de figure à envisager : k est multiple de 6, k n'est pas multiple de 6. Et le cas "k n'est pas multiple de 6" s'arrête là car l'hypothèse "si k est multiple de 6" n'est pas vérifiée donc n'a pas lieu d'être traitée.
- Si elle porte sur "k est multiple de 6", alors les cas de figure peuvent être (par exemple) "k est multiple de 6 mais pas de 5" et "k est multiple de 6 et de 5", mais dans la situation présente cela n'offre pas beaucoup d'intérêt
Je n'enseigne pas au collège ; mais je pense qu'à ce niveau (collégien), je dirai qu'on ne considère que la situation où l'hypothèse "si..." est vérifiée, car les autres n'ont pas d'objet. Je monterai également avec deux exemples que dans le cas où l'hypothèse n'est pas vérifiée, la conclusion n'est pas garantie (prendre k=3 et k=4).
A partir de la seconde, je commence à indiquer qu'une proposition de type "si H alors C" est vraie quand l'hypothèse H est fausse. pour faire "comprendre" cela je prend souvent des exemples tirés de la vie de tous les jours, par exemple en utilisant un argument de type "absurde" comme "c'est ça et moi je suis le pape", qui est un argument utilisé pour indiquer à son interlocuteur qu'on ne croit pas ce qu'il dit ("si ce que tu dis est vrai, alors je suis le pape" ; ceci pour arriver au fait qu'en mathématiques "Si H alors C" est vraie quand H est fausse.
En terminale (spécialité maths), je fais les tables de vérité.
Cela répond-il à ta question ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: signification de la phrase "Soit x appartient à E"
Oui, merci hdci,
en fait toutes les discussions sur l'implication dépendent de l'enseignement reçu.
Le si A alors B qui embarque de A faux ne fait pas partie de ma culture.
Enfin je l'ai appris sur le site il ya de nombreuses années, et tout va bien.
L'ai-je eu en enseignement terminal, je n'ai aucun souvenir.
De sorte que les quantificateurs devant l'implication me laissent perplexe.
Pour moi: pour k impair si k est multiple de 6 … n'a juste aucun sens …
Je serais très curieux de voir les quantificateurs devant une implication, utilisés pendant mon enseignement collège lycée.
Bref, tout dépend de l'enseignement. Donc merci de tes précisions parce que sur l'implication et son enseignement au lycée il me semble avoir tout entendu.
Pour en revenir au soit x
alors cela pouvait simplement dire x appartient à et là si x patati
x était juste défini réel ou autre et le si A...embarquait les x vérifiant A .
en fait toutes les discussions sur l'implication dépendent de l'enseignement reçu.
Le si A alors B qui embarque de A faux ne fait pas partie de ma culture.
Enfin je l'ai appris sur le site il ya de nombreuses années, et tout va bien.
L'ai-je eu en enseignement terminal, je n'ai aucun souvenir.
De sorte que les quantificateurs devant l'implication me laissent perplexe.
Pour moi: pour k impair si k est multiple de 6 … n'a juste aucun sens …
Je serais très curieux de voir les quantificateurs devant une implication, utilisés pendant mon enseignement collège lycée.
Bref, tout dépend de l'enseignement. Donc merci de tes précisions parce que sur l'implication et son enseignement au lycée il me semble avoir tout entendu.
Pour en revenir au soit x
alors cela pouvait simplement dire x appartient à et là si x patati
x était juste défini réel ou autre et le si A...embarquait les x vérifiant A .
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
En fait tu as peut-être vu au lycée la forme suivante (je prends ici un exemple définissant la racine carrée pour introduire la disjonction de cas "appartient à / n'appartient pas à") :
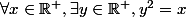
Qui est en fait équivalente à
))
Ou même quand on est en théorie des ensembles ZFC (puisqu'alors tout objet mathématique est un ensemble)
))
Finalement, pour en revenir au multiple de 6, on pourrait écrire
"Pour tout k multiple de 6, k est pair" ou bien "tout entier k multiple de 6 est pair"
Au lieu de
"Pour tout entier k, si k multiple de 6 alors k est pair"
Qui est en fait équivalente à
Ou même quand on est en théorie des ensembles ZFC (puisqu'alors tout objet mathématique est un ensemble)
Finalement, pour en revenir au multiple de 6, on pourrait écrire
"Pour tout k multiple de 6, k est pair" ou bien "tout entier k multiple de 6 est pair"
Au lieu de
"Pour tout entier k, si k multiple de 6 alors k est pair"
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: signification de la phrase "Soit x appartient à E"
Salut hdci,
oui culturellement la premiere proposition me parle.
ainsi que la prermiere pour les multiples de 6.
Surtout que la forme "pour tout truc", mon reflexe d'opposition renverserment est " il existerait pas"? ...
oui culturellement la premiere proposition me parle.
ainsi que la prermiere pour les multiples de 6.
Surtout que la forme "pour tout truc", mon reflexe d'opposition renverserment est " il existerait pas"? ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
Pour le dire autrement hdci:
on peut très bien dire:
soit k entier pour dire juste k appartient IN,
si k pair alors k multiple de 6
ce truc dit "pour tout" k pair alors j'ai k multiple de 6
Et c'est faux car" il existe" les k pairs non multiples de 6 qui ne vérifient pas multiple de 6
On voit bien que le "il existe" qui inverse le" pour tout", il est pris dans les k pair
Si on note chez les petits une écriture de grands:
"Pour tout" k entier, si k pair alors k multiple de 6
Le "il existe" qui rend faux le " pour tout", ben c'est pas au niveau du pour tout k entier,
il existe des k impairs non multiples de 6 qui n'ont rien à voir avec ce que l'on veut démontrer ou infirmer.
Donc perso au niveau ensembliste je trouve cela très déstabilisant pour les apprentissages.
Donc la question, car sur ce forum dès que l'on discute on est catalogué dans un camp,
est bien pour les petites classes,
c'est quoi l'implication, avec quels quantificateurs, placés où?
Car la résultante de tout ceci est tantot il ne faut pas utiliser l'implication au lycée (= pas tant qu'on n'a pas vu avec le A faux),
et tantot, ben la solution c'est pas de quantificateurs dans petites classes. Sauf que sans quantificateur comment apprend-on que le " pour tout" ne marche pas quand "il existe" qui me semble assez fondamental.
Enfin bref hdci, je ne suis pas enseignant, et je ne fais que discuter.
on peut très bien dire:
soit k entier pour dire juste k appartient IN,
si k pair alors k multiple de 6
ce truc dit "pour tout" k pair alors j'ai k multiple de 6
Et c'est faux car" il existe" les k pairs non multiples de 6 qui ne vérifient pas multiple de 6
On voit bien que le "il existe" qui inverse le" pour tout", il est pris dans les k pair
Si on note chez les petits une écriture de grands:
"Pour tout" k entier, si k pair alors k multiple de 6
Le "il existe" qui rend faux le " pour tout", ben c'est pas au niveau du pour tout k entier,
il existe des k impairs non multiples de 6 qui n'ont rien à voir avec ce que l'on veut démontrer ou infirmer.
Donc perso au niveau ensembliste je trouve cela très déstabilisant pour les apprentissages.
Donc la question, car sur ce forum dès que l'on discute on est catalogué dans un camp,
est bien pour les petites classes,
c'est quoi l'implication, avec quels quantificateurs, placés où?
Car la résultante de tout ceci est tantot il ne faut pas utiliser l'implication au lycée (= pas tant qu'on n'a pas vu avec le A faux),
et tantot, ben la solution c'est pas de quantificateurs dans petites classes. Sauf que sans quantificateur comment apprend-on que le " pour tout" ne marche pas quand "il existe" qui me semble assez fondamental.
Enfin bref hdci, je ne suis pas enseignant, et je ne fais que discuter.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
Bonjour,
) est une abréviation pour
est une abréviation pour )) .
.
) est une abréviation pour
est une abréviation pour )) .
.
Re: signification de la phrase "Soit x appartient à E"
beagle a écrit:on peut très bien dire:
soit k entier pour dire juste k appartient IN,
si k pair alors k multiple de 6
ce truc dit "pour tout" k pair alors j'ai k multiple de 6
Et c'est faux car" il existe" les k pairs non multiples de 6 qui ne vérifient pas multiple de 6
Oui c'est d'ailleurs un exemple qui montre que si une cause provoque une conséquence, ladite conséquence ne provoque pas forcément la cause.
A des élèves de seconde qui me demandaient un exemple d'implication qui n'est pas une équivalence, je citais souvent "si x =2 alors x²=4", mais la réciproque "si x²=4 alors x=2" et fausse puisque x peut être égal à -2.
Maintenant, j'enseigne en lycée et fait des colles en MPSI, donc je n'ai pas le problème de tenter de faire comprendre cela à des "petits". Mais ce que je constate chez les secondes, c'est que pour certain la notion de quantificateur n'est pas bien comprise, beaucoup continuent de raisonner en prenant des exemples qui marchent (là où on est dans du "quel que soit"). Pour leur faire comprendre que ce raisonnement ne fonctionne pas, je prends l'exemple de la classe dans laquelle j'affirme que "tous les élèves sont des filles", et je prend un, deux, trois, quatre exemples (pour bien montrer que c'est vrai pour des tas d'exemples, mais que ma conclusion est évidemment fausse - enfin tant que j'ai des classes mixtes bien sûr...).
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: signification de la phrase "Soit x appartient à E"
Un petit bonjour hdci,
je sais que tu ne te meles pas du pugilat sur l'autre fil de discussion,
mais pourquoi on ne pouvait pas embarquer les memes quantificateurs en version soft de l'implication du si A vrai alors …
lycee/implication-logique-t217805-60.html#p1463467
les demandes d'exos de GBZM sont à voir.
je sais que tu ne te meles pas du pugilat sur l'autre fil de discussion,
mais pourquoi on ne pouvait pas embarquer les memes quantificateurs en version soft de l'implication du si A vrai alors …
lycee/implication-logique-t217805-60.html#p1463467
les demandes d'exos de GBZM sont à voir.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
beagle a écrit:mais pourquoi on ne pouvait pas embarquer les memes quantificateurs en version soft de l'implication du si A vrai alors …
Là je ne comprends pas vraiment ce que tu veux dire : "version soft" ? "embarquer les mêmes quantificateurs" ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: signification de la phrase "Soit x appartient à E"
Euh Beagle, je sais que tu es en manque de soutien mais quand même, essayer de faire se confronter hdci avec moi (ou GaBuZoMeu ou d'autres) est voué à l'échec. Je suis d'accord avec lui, je trouve que ses interventions sont claires et je n'ai aucune prétention à faire mieux que lui.
Ceci étant dit, si tu veux poser des questions à quelqu'un en particulier, s'il accepte de te répondre et si tu arrives à entendre ses réponses sans avoir l'attitude que je te reproche, je n'interviendrai pas, je n'y vois aucun inconvénient, au contraire, j'en serai ravie.
@hdci Désolée, je vous laisse discuter, Beagle n'accepte pas que je me moque de lui quand il a ce genre de propos
"Embarquer du A vrai dans un si A alors...est une convention d'écriture et d'usage.
Qui a existé qui existe ...
On peut imposer un autre usage une autre écriture mais c'est pas la peine pour autant de faire la blonde."
"C'est dommage que la présentation plus large de l'implication ... soit en opposition avec le si A alors B plus simple avec le A vrai qui est un objet mathématique collège lycée qui fonctionne."
Après les multiples discussions à ce sujet où je lui ai expliqué que l'implication est toujours la même du collège au supérieur.
Ceci étant dit, si tu veux poser des questions à quelqu'un en particulier, s'il accepte de te répondre et si tu arrives à entendre ses réponses sans avoir l'attitude que je te reproche, je n'interviendrai pas, je n'y vois aucun inconvénient, au contraire, j'en serai ravie.
@hdci Désolée, je vous laisse discuter, Beagle n'accepte pas que je me moque de lui quand il a ce genre de propos
"Embarquer du A vrai dans un si A alors...est une convention d'écriture et d'usage.
Qui a existé qui existe ...
On peut imposer un autre usage une autre écriture mais c'est pas la peine pour autant de faire la blonde."
"C'est dommage que la présentation plus large de l'implication ... soit en opposition avec le si A alors B plus simple avec le A vrai qui est un objet mathématique collège lycée qui fonctionne."
Après les multiples discussions à ce sujet où je lui ai expliqué que l'implication est toujours la même du collège au supérieur.
Re: signification de la phrase "Soit x appartient à E"
La version soft c'est l'implication qui utilise un si A
avec A vrai implicite
donc tu ne peux pas mettre un quantificateur qui rend faux ton A vrai.
Le quantificateur embarque tous les A vrais, et eux seulement.
avec A vrai implicite
donc tu ne peux pas mettre un quantificateur qui rend faux ton A vrai.
Le quantificateur embarque tous les A vrais, et eux seulement.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
et bien le marquage à la culotte de la blonde, l'autre fil de discussion ne te suffit pas?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
Chose promise, chose due, j'interviens dès que tu dis n'importe quoi en attendant que tu arrêtes de dire n'importe quoi, à bientôt 
Re: signification de la phrase "Soit x appartient à E"
Répond à cette question toi qui sait tout:
Y avait-il oui ou non au lycée un usage du si A alors B
qui sans avoir à le dire utilisait uniquement du A vrai,
implicite= pas besoin de le préciser
il ya quelques décennies
1) c'est vrai
2) c'est faux
3) je sais pas je suis trop jeune
4) autre
Y avait-il oui ou non au lycée un usage du si A alors B
qui sans avoir à le dire utilisait uniquement du A vrai,
implicite= pas besoin de le préciser
il ya quelques décennies
1) c'est vrai
2) c'est faux
3) je sais pas je suis trop jeune
4) autre
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: signification de la phrase "Soit x appartient à E"
Je ne sais pas, je suis trop jeune mais j'ose espérer que c'est faux car c'est n'importe quoi comme manière de faire. Il faut toujours préciser, on a A, on utilise le théorème A=>B donc on a démontré B et même au collège, cela me semble largement exigible.
Re: signification de la phrase "Soit x appartient à E"
Au lieu de répéter en boucle
Peux-tu donner un exemple précis, documenté (ex : un extrait de manuel). Comme ça, on pourra discuter sur du concret, pas dans le flou.
Y avait-il oui ou non au lycée un usage du si A alors B
qui sans avoir à le dire utilisait uniquement du A vrai,
implicite= pas besoin de le préciser
Peux-tu donner un exemple précis, documenté (ex : un extrait de manuel). Comme ça, on pourra discuter sur du concret, pas dans le flou.
69 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
