[Spé] Reste d'une division euclidienne
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 17 Sep 2006, 19:14
par babaz » 17 Sep 2006, 19:14
Bonsoir,
J'ai un exerice qui me demande de trouver le reste de
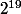
par 11.
J'ai cru comprendre que pour parvenir à une "congruence finale", je devais plus ou moins effectuer 2 par 11, ce qui me donnerait
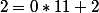
Comment, à partir de là, puis-je trouver le reste (en l'occurrence 4) ?
Merci beaucoup
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 17 Sep 2006, 19:22
par zebdebda » 17 Sep 2006, 19:22
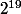
plutôt non ?
Alors la méthode consite à d'abord trouver une puissance de 2 congrue à 1 modulo 11.
Pour cela 2 méthodes : calculer les puissances successives
ou Alors : par Fermat 2^10 est congru à 1 modulo 11 car 11 est premier
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 17 Sep 2006, 19:24
par babaz » 17 Sep 2006, 19:24
Je n'ai rien compris.
Merci quand même
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 17 Sep 2006, 19:40
par zebdebda » 17 Sep 2006, 19:40
Tu n'as pas encore vu le théorème de Fermat peut-être...
Sinon ça n'est pas grave.
Suis mes instructions je te donne les étapes intermédiaires.
Calcule le reste par la division euclidienne par 11 des puissances successives de 2 (
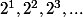
)
jusqu'à trouver comme résultat 1 ou -1.
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 17 Sep 2006, 20:23
par babaz » 17 Sep 2006, 20:23
Malgré ces explications supplémentaires, je ne vois toujours pas bien comment faire.
Peux-tu me dire encore plus précisément où tu veux en venir ?
Merci
-
sbz
- Membre Relatif
- Messages: 174
- Enregistré le: 01 Mai 2005, 10:00
-
 par sbz » 17 Sep 2006, 20:26
par sbz » 17 Sep 2006, 20:26
babaz a écrit:Malgré ces explications supplémentaires, je ne vois toujours pas bien comment faire.
Peux-tu me dire encore plus précisément où tu veux en venir ?
Merci
l'idée c'est de trouver une puissance de 2 congru à 1 ou -1 mod 11 et d'écrire 2^19 avec une puissance de 2 congru à 1 et de faire sa de manière iterative ... à la fin tu auras une petite puissance de 2 où tu pourras trouver facilement le reste
ex: 2^5 == -1 [11]
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 17 Sep 2006, 20:28
par zebdebda » 17 Sep 2006, 20:28
une fois que tu as trouvé a tel que
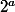
congru à 1 ou -1 modulo 11, on fais la division euclidienne de 19 par a.
Alors 19=aq+r, où r est plus petit que a (donc on sait déjà à quoi est congru
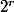
modulo 11)
Et donc
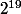
=
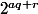
=
}^q 2^r)
qui sera congru à
}^q 2^r)
ou
}^q 2^r)
ce qui devient très facile à calculer.
Mais je ne voulais pas t'expliquer tout de suite toute la théorie (trop dure à encaisser, on ne voit pas beaucoup plus où on va) : mieux vaut traiter l'exemple au fur et à mesure, ainsi que je voulais te le faire faire
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 17 Sep 2006, 20:46
par babaz » 17 Sep 2006, 20:46
Merci, mais franchement, en "spé", est-on obligé d'apprendre des méthodes de ce type "par coeur" (c'est bien le terme) ?
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 17 Sep 2006, 20:51
par zebdebda » 17 Sep 2006, 20:51
euh... et oui malheureusement !
Rassure-toi il y aura peu de méthode si détaillées à apprendre par coeur, et tu vas les appliquer tellement qu'elles rentreront toutes seules.
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 17 Sep 2006, 20:57
par babaz » 17 Sep 2006, 20:57
"En mathématiques, on ne comprend pas les choses, on s'y habitue."
John von Neumann
-
zebdebda
- Membre Relatif
- Messages: 470
- Enregistré le: 16 Sep 2006, 15:35
-
 par zebdebda » 17 Sep 2006, 20:58
par zebdebda » 17 Sep 2006, 20:58
perso j'ai compris toutes ces méthodes ! tu peux le faire aussi !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
