Bonjour,
SVP \int_{0}^{1}{dx}\frac{1}{x^{3}+3x+2}, quelqu'un sait comment résoudre cette intégrale?
Merci !!
Résoudre une intégrale
8 messages
- Page 1 sur 1
Re: Résoudre une intégrale
Bonjour
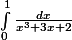
La difficulté provient du fait que la seuleracine réelle du dénominateur est compliquée, c'est :
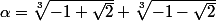
Cela permet de factoriser ce dénominateur
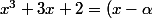(x^2+\alpha x+{\alpha}^2+3))
et donc ensuite de décomposer la fonction en somme de fonctions "facilement" intégrables....
La difficulté provient du fait que la seuleracine réelle du dénominateur est compliquée, c'est :
Cela permet de factoriser ce dénominateur
et donc ensuite de décomposer la fonction en somme de fonctions "facilement" intégrables....
Re: Résoudre une intégrale
Bonjour,
Je vois ce que vous voulez dire. Mais comment vous avez fait pour trouver la racine du dénominateur?
Je vois ce que vous voulez dire. Mais comment vous avez fait pour trouver la racine du dénominateur?
Re: Résoudre une intégrale
Bonjour,
Etes-vous sûre des signes ? Car si au dénominateur on avait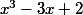 , alors il y a une factorisation évidente par
, alors il y a une factorisation évidente par ) .
.
Sinon, trouver les racines d'un polynômes du 3ème degré est quelque chose de compliqué, avec à la clef les formules de Cardan, mais il me semble surprenant d'avoir ce type de question au niveau "lycée".
Etes-vous sûre des signes ? Car si au dénominateur on avait
Sinon, trouver les racines d'un polynômes du 3ème degré est quelque chose de compliqué, avec à la clef les formules de Cardan, mais il me semble surprenant d'avoir ce type de question au niveau "lycée".
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Résoudre une intégrale
C'est sûrement le signe. Vous devez avoir raison, c'est beaucoup trop compliqué . En tout cas, merci à vous deux!
Re: Résoudre une intégrale
Bonjour,
Oui, il y a vraisemblablement une erreur d'énoncé (qui n'est pas le signe du terme en x du dénominateur ... qui donne effectivement une intégrale divergente)
Si on veut s'amuser à trouver des énoncés probables (parmi une infinité) au niveau Lycée, on peut par exemple choisir :


Oui, il y a vraisemblablement une erreur d'énoncé (qui n'est pas le signe du terme en x du dénominateur ... qui donne effectivement une intégrale divergente)
Si on veut s'amuser à trouver des énoncés probables (parmi une infinité) au niveau Lycée, on peut par exemple choisir :
Re: Résoudre une intégrale
C'était peut-être 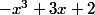 au dénominateur, ou
au dénominateur, ou 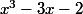
Quoi qu'il en soit, au niveau terminal l'exercice est osé, la décomposition d'une fraction rationnelle en éléments simples n'étant pas au programme.
Quoi qu'il en soit, au niveau terminal l'exercice est osé, la décomposition d'une fraction rationnelle en éléments simples n'étant pas au programme.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
