Résolution d'une équation du second degré

[toitoine-78]

Bonjour,

Je suis en seconde et notre professeur, nous a donné un devoir maison où jusqu'ici, j'avais tout réussi.

Mais pour cette exercice, nous n'avons jamais vu cela en cours et j'aimerai si possible avoir des explications...

Soit g la fonction définie par: g: R --> R On souhaite trouver les antécédents de 0 par g.
x --> x²+x-1

1) Montrer que cela est équivalent à résoudre l'équation x²+x-1=0
Cette équation est appelée équation du second degré à cause de la présence du carré de x.

2) Montrer que x²+x-1=(x+1/2)²-5/4

3) Factoriser cette expression en utilisant une identité remarquable, puis résoudre l'équation x²+x-1=0

4) En déduire les antécedents de 0 par g.

Merci d'avance à ceux qui vont pouvoir m'aider. ;D

[oscar]

bjr

tu pouvais directement
écrire

x² + x - 1 =0 déterminer les racines
D = 1+4 =5
les antécédents sont (-1 +v 5)2 et (-1-v5)/2

Tu peux vérifier (-1+v5)²/4 + ( -1+v5) /2 -1=0

[toitoine-78]

Bonjour, cette réponse est valable que pour la question 2) ou pas ?

Pourrais tu m'expliquer la 1)

Merci =)

[toitoine-78]

Bonjour,

Pourriez-vous me donner les réponses car en effet c'est urgent.

Merci d'avance à vous tous.

[toitoine-78]

S'il vous plaît au moins une piste. :/

[Jimm15]

Bonjour,

Chercher l’image par de 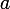revient à chercher .
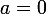Par exemple, si et qu’on souhaite obtenir l’image de par , on remplace simplement : .
L’image de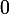 par est donc .

Chercher l’ (les) antécédent(s) de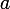 par revient à déterminer 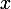tel que .
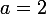Par exemple, si et qu’on souhaite obtenir l’ (les) antécédent(s) de par , on résout :




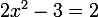
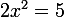
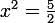
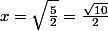ou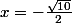
Les antécédents de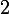 par sont donc 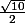et .

Remarque : Il ne peut y avoir qu’une seule image mais il peut y avoir plusieurs antécédents.