Résolution é'une equation de forme cos(x) = a

[passio]

Bonjour, j'ai appris la semaine dernière à résoudre des équations comme : cos(x)= (V3)/2

ou encore
2sin(x) = 1 (=) sin(x) = 1/2


Ce sont à chaque fois des valeurs remarquables, sauf que là j'ai un exercice qui dit : Résoudre dans R puis dans [0; 2PI], l'équation : cos(3x)= -0.715

Le problème c'est que ce n'est pas une valeur remarquable, et que je ne sais pas comment m'y prendre car nous n'avons pas encore fait le cours, j'aimerais connaître la méthode pour résoudre l'équation dans R. Merci

[Clembou]

Bonjour, j'ai appris la semaine dernière à résoudre des équations comme : cos(x)= (V3)/2

ou encore
2sin(x) = 1 (=) sin(x) = 1/2


Ce sont à chaque fois des valeurs remarquables, sauf que là j'ai un exercice qui dit : Résoudre dans R puis dans [0; 2PI], l'équation : cos(3x)= -0.715

Le problème c'est que ce n'est pas une valeur remarquable, et que je ne sais pas comment m'y prendre car nous n'avons pas encore fait le cours, j'aimerais connaître la méthode pour résoudre l'équation dans R. Merci

Il faut que tu linéarise le avec les formules d'addition trigonométriques. Remarques que par exemple

[passio]

:doh:
Sans mauvaise volonté, je ne vois vraiment pas où celà mêne... J'ai travaillé une seule heure sur les équations de ce type... Pourriez vous me guider un peu plus?

[Ericovitchi]

ou bien tu poses cos(a)= -0.715 (et tu trouves a avec une calculatrice)
et puis tu en déduis 3x= plus ou moins a + 2Kpi, etc...

[passio]

Ok, je vais faire cette méthode alors, merci beaucoup.

J'ai un dernier exercice, il s'appelle exercice 3* d'ailleurs :triste:

1)Factoriser 2X² - X - 1 (Je sais pas faire du tout :hein: )
2)En déduire la relation dans R de l'équation 2cos²x - cos x - 1 = 0. (non plus)

Pourriez vous m'aider pour celui là... Je suis qu'en seconde et mon ami en 1ère S à pas su m'aider :dodo:

[Ericovitchi]

pour factoriser dans un cas comme ça, il faut calculer les deux racines et écrire le polynôme a(x-x1)(x-x2)
Tu as appris à calculer les racines d'un polynôme du second degré ?

[Ericovitchi]

non attends, il y a une méthode plus facile.

Remarques que x=1 annule le polynome. Donc x-1 va pouvoir se mettre en facteur.

Essayes d'écrire le polynôme sous la forme 2(x-1)(x-?)

[passio]

Non, pas du tout... J'ai une classe avec 10 personnes au dessus de 16 de moyenne en Maths, donc... On a des trucs un peu plus difficile... J'ai jamais entendu polynôme de ma vie en cours...

[passio]

Je crois que je vais laisser tombé, je n'y comprends rien... Il a mis une étoile à l'exercice je viens de comprendre pourquoi...

PS: C'est X pas x... (si c'est important ?)

[Ericovitchi]

Ca n'est pas si dur que ça. Regardes :
On sait que x=1 est une solution et que donc on va pouvoir mettre x-1 en facteur :

Je commence à mettre (x-1)(?
et je me demande par quoi je vais multiplier pour faire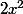 ? --> par 2x pardi

Donc j'en suis ) (x-1)(2x+?)
Et là je me dis je dois faire un -x mais quand je multiplie -1 par 2x ça me fait un -2x donc il faut que je génère un +x pour compenser et donc le deuxième facteur est +1
(x-1)(2x+1) Voilà le résultat

[passio]

J'ai à peu près compris oui, c'est surtout polynome qui m'effrayait... J'essaye de faire la 2 seul en attendant.

[passio]

Alors :

2X² - X - 1
(X-1)(2X+1)

2cos²x - cos x - 1 = 0
d'où :
(cos(x)-1)(2cos(x)+1) = 0 si :

cos(x) - 1 = 0 . . . ou . . . 2cos(x)+1 = 0
cos(x) = 1 . . . . .. ou . . . 2cos(x) = -1
. . . . . . . . . . . . . . . . . . cos(x) = -1/2


x = 0+k2;). . . . . . . ou . . . . . . . x = /3 + k2;)
x = 2;)+k2;) . . . . . . ou . . . . . . x = -;)/3 + k2;) . . . . . (avec k € Z)


C'est ça :peur: ?

Edit : Non pour cos(x) = -1/2

[Ericovitchi]

pas tout à fait, il y a une erreur de signe.

D'abord le cos(x)=1 OK pour x=k2pi
(pas la peine de mettre 2pi+k2pi)

2cos(x)+1 = 0 --> cos(x) = -1/2 (il y avait une faute de signe)
il faut trouver un cos(a) qui vaut -1/2 donc par exemple 2pi/3

puis utiliser cos(x)=cos(a) --> x=a + k2pi ou x=-a + k2pi

[passio]

x = 0+k2;). . . . . . . et . . . . . . . x = 2;)/3 + k2;)
. . . . . . . . . . . . . . . . . . . . . . ou . x = 4;)/3 + k2;) . . . . . (avec k € Z)


Voilà, c'est bon j'ai trouvé, j'ai vérifié et (normalement) ça marche ! Merci beaucoup pour ton aide en tout cas, je reviendrais sûrement une prochaine fois ! Bonne fin de journée et un grand merci.