Résolution équations - Seconde
14 messages
- Page 1 sur 1
Résolution équations - Seconde
Bonsoir à tous.
C'est mon premier post pour une aide en maths,grande première (et euh désolée j'ai pas encore réussi à me servir des balises TEX (lol) , mais je vais m'entraîner!
Voilà, j'aurai besoin de votre aide pour un exercice de résolutions d'équations, j'en ai réussi 4 sur 7 je pense mais là je bloque...
Résoudre dans IR en jonglant avec les développements et factorisations:
(2x+3)(x-3)+x(x+3)=0
2x(x+3)-(x+1)^2=11 (en s'aidant du fait que (x+1)^2-1=x^2+2x)
et enfin: (3x+1)^2-(4x-2)^2=0
Merci d'avance de vos réponses...
C'est mon premier post pour une aide en maths,grande première (et euh désolée j'ai pas encore réussi à me servir des balises TEX (lol) , mais je vais m'entraîner!
Voilà, j'aurai besoin de votre aide pour un exercice de résolutions d'équations, j'en ai réussi 4 sur 7 je pense mais là je bloque...
Résoudre dans IR en jonglant avec les développements et factorisations:
(2x+3)(x-3)+x(x+3)=0
2x(x+3)-(x+1)^2=11 (en s'aidant du fait que (x+1)^2-1=x^2+2x)
et enfin: (3x+1)^2-(4x-2)^2=0
Merci d'avance de vos réponses...
Bonsoir à tous,
Pour la deuxième 2x(x+3)-(x+1)^2=11 , je ne comprends pas pourquoi "l'astuce" (x+1)^2 - 1 = x^2 + 2x est donnée. Elle est même plutôt nuisible à mon sens car elle empêche d'avoir une démarche générale.
En fait, on peut toujours "factoriser" une équation du second degré (sur si
si 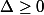 , sur
, sur  sinon...) Cela s'appelle la forme canonique. C'est ni plus ni moins qu'une identité remarquable du type
sinon...) Cela s'appelle la forme canonique. C'est ni plus ni moins qu'une identité remarquable du type (a+b)) .
.
Si tu développes, tu trouves
L'astuce de la forme canonique est de reconnaître le début d'un carré dans . C'est en fait
. C'est en fait ^2 - 4) .
.
Tu obtiens donc l'équation^2 - 16 = 0) , que tu sais résoudre (utilise
, que tu sais résoudre (utilise (a+b)) ).
).
PS: la même chose marche pour toutes les équations du second degré admettant des racines réelles, c'est ça l'avantage. Plus besoin de fausses astuces.
Luc
Pour la deuxième 2x(x+3)-(x+1)^2=11 , je ne comprends pas pourquoi "l'astuce" (x+1)^2 - 1 = x^2 + 2x est donnée. Elle est même plutôt nuisible à mon sens car elle empêche d'avoir une démarche générale.
En fait, on peut toujours "factoriser" une équation du second degré (sur
Si tu développes, tu trouves
L'astuce de la forme canonique est de reconnaître le début d'un carré dans
Tu obtiens donc l'équation
PS: la même chose marche pour toutes les équations du second degré admettant des racines réelles, c'est ça l'avantage. Plus besoin de fausses astuces.
Luc
Tout d'abord, merci à tous pour vos réponses.
Donc effectivement la note entre parenthèse devait vouloir nous mettre sur la piste de la forme canonique et de savoir repérer le début d'un carré.....je pense. J'ai compris grâce à vous et je trouve pour la 2ème x=-6 et x=2.
Mais je ne comprends pas pourquoi dans (3x+1)^2-(4x-2)^2=0 les réponses ne sont pas x=1/7 et x=-3? je l'ai refait et je trouve la même chose.
Sinon j'ai compris la méthode je pense. Encore merci.
Donc effectivement la note entre parenthèse devait vouloir nous mettre sur la piste de la forme canonique et de savoir repérer le début d'un carré.....je pense. J'ai compris grâce à vous et je trouve pour la 2ème x=-6 et x=2.
Mais je ne comprends pas pourquoi dans (3x+1)^2-(4x-2)^2=0 les réponses ne sont pas x=1/7 et x=-3? je l'ai refait et je trouve la même chose.
Sinon j'ai compris la méthode je pense. Encore merci.
neferet a écrit:Tout d'abord, merci à tous pour vos réponses.
Donc effectivement la note entre parenthèse devait vouloir nous mettre sur la piste de la forme canonique et de savoir repérer le début d'un carré.....je pense. J'ai compris grâce à vous et je trouve pour la 2ème x=-6 et x=2.
Mais je ne comprends pas pourquoi dans (3x+1)^2-(4x-2)^2=0 les réponses ne sont pas x=1/7 et x=-3? je l'ai refait et je trouve la même chose.
Sinon j'ai compris la méthode je pense. Encore merci.
Cool que tu aies compris. Attention au signe pour x=-3. Les solutions sont bonnes pour la 2ème.
Luc
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
