Résolution équation logarithme

[Tunez]

Bonjour, j'aimerais avoir une petite aide sur un exercice :
Je dois donner le domaine de définition et résoudre l'expression suivante :
(ln(x))² +3ln(x) -10 =0
Le domaine de définition que j'ai trouvé c'est x>0 car ln ne peut pas être égal à 0 mais je pense me tromper là dessus

J'ai fait ça, je pense que c'est juste mais j'en suis pas certain
On pose X =ln(x)
Donc X² +3*X -10 =0
J'ai ensuite utilisé delta :
b²- 4ac = 3² - 4*1*(-10) = 9+40 =49
Delta > 0
donc x1= (-3 -49^(1/2)) / 2*1 = -5
x2= (-3 +49^(1/2)) / 2*1 = -2

J'ai écris la racine de 49 avec 49^(1/2) je ne sais pas comment faire la racine
Mais j'ai 2 solutions inférieur à 0 du coup je bloque et je ne sais pas ou est ce que j'ai faux.
Merci d'avance :lol3:

[Ericovitchi]

Et alors ? il y a des solutions à ln (x) = -2 et ln(x) = -5
ça peut être négatif un log

[Tunez]

Oui mais mon domaine de définition c'est ]0;+infini[ (x>0) du coup -2 et -5 ne peuvent pas être des solutions pour le domaine de définition que j'ai

[capitaine nuggets]

Salut !

Tu confonds l'ensemble de définition de la fonction ln et les images qu'elle peut prendre.

Je te rappelle que bien que la fonction ln n'est définie que sur , on a :
1) pour tout .

Par exemple,

[Tunez]

Oui mais du fait que j'ai un ensemble de définition de ]0;+infini[ -2 et -5 ne sont pas des solutions de mon équation, ce sont des images possible mais pour autant pas des solutions non ?
On en a fait d'autres en cours des résolutions d'équations comme ça, si les solutions trouvées n'était pas comprises dans l'ensemble de définition déterminé auparavant alors ont les laissaient tomber et ont gardaient celles qui étaient comprises dans l'intervalle. Mais là j'en ai aucune de comprises dans l'intervalle. Je ne peut pas remplacer x par -2 ou -5 car ln(-2) ou ln(-5) c'est impossible.
Merci de vos réponses

[capitaine nuggets]

Ah, je crois avoir compris ton problème.
En fait, tu voudrais bien écrire .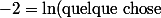
Pour cela, il suffit de savoir que quel que soit , .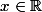
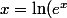En effet,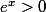 , quel que soit réel donc le fait d'écrire a bien un sens.

:we: