[Résolu] Reecriture de nombres

par **smile** » 03 Mai 2009, 13:52

Salut,
Excusez le fait que j'arrive un peu comme un opportuniste, mais j'ai vraiment besoin d'aide. Je bloque sur une réecriture:
J'ai ce nombre là:

Je dois le réecrire sous la forme:

où alpha, beta et gamma sont des réels.
Et je n'y arrive pas :cry:

Si vous avez des idées...

Merci d'avance

par **Le Chaton** » 03 Mai 2009, 14:08

Bonjour ,
HAN un opportuniste XD :p :p
Essaye de mettre

Au même dénominateur ( donc sur x+2) et ensuite tu identifies...
ça te donnera un système :
"tout ce qui y'a devant les x²" = 2
"tout ce qui y'a devant les x " = -3
"et tous les chiffres " = 1

par **Cheche** » 03 Mai 2009, 14:10

Salut,

smile a écrit:Je dois le réecrire sous la forme:

où alpha, beta et gamma sont des réels.

On appelle cela décomposer en éléments simples d'une fraction rationnelle.

Fraction rationnelle :

Éléments simples :

ou

Deux méthodes :

- La première : "par identification"
Tu mets au même dénominateur la décomposition en éléments simples (

).
Tu égalises avec l'expression de départ.
Tu "identifies" les coefficients devant chaque terme (devant x^2, devant x et devant 1).
Tu aurais donc un système de trois équations à trois inconnues à résoudre.

- La deuxième : "par division euclidienne"
Tu fais la division euclidienne de deux polynômes :

par le polynôme

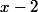
Remarque : Si tu ne connais pas la division euclidienne de deux polynômes, fait la première méthode.

par **Ericovitchi** » 03 Mai 2009, 14:22

Et puis tu as la méthode Pro si tu as le goût de l'aventure :
tu écris

Et là tu te dis :
Cette expression doit être vraie pour tout x donc :
Si je multipliais à gauche et à doite par (x-2) et que je faisais x=2
ça ferait

donc

Si je fais x=0

Si je divisais à gauche et à droite par x et que je faisais tendre x vers l'infini

Et voilà comment on trouve les coefficients pratiquement sans calculs.

par **smile** » 03 Mai 2009, 14:25

Merci pour vos réponses,
En revanche j'ai du mal à vous suivre. Je suis en 1ere ES et je me souviens pas d'avoir fait des choses aussi complexes :fr:

J'ai mis en facteur commun et j'obtiens ca:

En revanche vous me parlez de mettre en équation avec les coefficients (2, -3 et 1 si j'ai bien compris) et c'est là que je vous suis plus. :hein:

par **Le Chaton** » 03 Mai 2009, 14:30

Euh nan c'est pas ça ...

= ??

par **smile** » 03 Mai 2009, 14:38

Je suis vraiment perdu. L'expression que tu me donne Le Chaton c'est une équation ? Comment je suis censé resoudre une equation à 2 inconnus avec une seule expression ?
Je sais que

est egale à 1 (enfin je crois) ...
Quand je penses que c'est juste la première question :cry:

par **Le Chaton** » 03 Mai 2009, 14:40

Non ce que j'essaye de te faire comprendre c'est que tu t'es trompé en mettant tout sur le même dénominateur tout à l'heure ... ( et oui (x-2)/(x-2)=1 ... c'est ça le principe pour mettre sur le même dénominateur ... on multiplie par 1 donc ça change pas ... mais on a une opération différente )

par **smile** » 03 Mai 2009, 14:49

Bon ok j'ai ax que je mets en fraction sur x-2 ce qui donne:

donc

Non ?

par **Le Chaton** » 03 Mai 2009, 14:52

Non pas du tout .
Moi je trouve

par **Ericovitchi** » 03 Mai 2009, 14:53

non

Et

, il a disparu ?

par **smile** » 03 Mai 2009, 14:57

Ca deviens grave :mur:
Je faisais une fixation (a + x) (x + 2) ce qui change la donne en fait.

Merci de te montrer aussi patient

edit: donc ca fait

par **Le Chaton** » 03 Mai 2009, 15:00

Ericovitchi a écrit:non

Et , il a disparu ?

( Pour le

il l'a bien fait ... c'est pour cela que j'ai pris que la partie la de l'opération .... :p mais maintenant qu'il a vu sa tite faute il peut refaire les trois équations !!

enfin son système ... :p )

par **smile** » 03 Mai 2009, 15:14

Chaud le boulet que je suis :triste:
Vous pouvez me dire a quoi mon systeme d'equation doit ressembler ?
C'est vraiment la première fois que je fais ca, je suis dans l'espace, l'ultime frontière, etc.

par **Le Chaton** » 03 Mai 2009, 15:16

En fait dans l'équation que tu trouves tu mets en facteur x² ( ça devrait être vite fait y'a qu'un seul truc en x² ... )
Tu mets en facteur tout ce qui est en x ...
et tu laisses toutes les lettres qui ne sont ni en x ni en x² ...
Et après c'est une identification ...

par **smile** » 03 Mai 2009, 15:21

Je ne te comprends toujours pas. Désolé.

par **Le Chaton** » 03 Mai 2009, 15:32

smile a écrit:Ca deviens grave :mur:
Je faisais une fixation (a + x) (x + 2) ce qui change la donne en fait.

Merci de te montrer aussi patient

edit: donc ca fait

Voila on part de ça :

Dans le numérateur de la fonction la tu mets tout ce qui y'a en x² en facteur ...
Ensuite tu mets tout ce qu'il y'a en x en facteur ...

je vais te prendre un exemple ...

Maintenant si on me dit que mon équation de départ devait être égale à

ça me fait un système du genre :
a+2*b=3
4*a-3*b=7
...

par **smile** » 03 Mai 2009, 16:14

bon je factorise:

On pose:

Ce qui donne :
alpha = 2
beta = 1
gamma = 3

Et ca marche!

Merci a tous :++:

PS: Où avez vous appris cette methode ? la question que j'ai posé viens d'un exercice "de synthèse" sur les limites sur une feuille (non corrigé) donné par notre prof. Je reste étonné par le raisonnement demandé :we:

par **Le Chaton** » 03 Mai 2009, 16:49

smile a écrit:bon je factorise:

On pose:

Ce qui donne :
alpha = 2
beta = 1
gamma = 3

Et ca marche!

Merci a tous :++:

PS: Où avez vous appris cette methode ? la question que j'ai posé viens d'un exercice "de synthèse" sur les limites sur une feuille (non corrigé) donné par notre prof. Je reste étonné par le raisonnement demandé :we:

A l'école :p
Si tu as tout compris c'est cool bonne fin de journée a toi

++

[Résolu] Reecriture de nombres

[Résolu] Reecriture de nombres

Qui est en ligne