La quantité conjuguée
20 messages
- Page 1 sur 1
La quantité conjuguée
Bonjour;
J'ai un exercice à effectué mais je ne le comprend pas.
1. Vérifier par le calcul que (√5 - √2)(√5 + √2 ) est un nombre entier.
En tapant ce calcul sur ma calculatrice je trouve 3 et 3 est un nombre entier. Faut-il que je developpe ce calcul ?
2. Pour ne plus avoir de racine carrée au dénominateur de A= 1/√5- √2' , Chloé propose de multiplier le numérateur et le dénominateur par √5+√2. Effectuer ce calcul puis conclure.
Le dénominateur disparaît est on obtiens 7, 480025655 ???
3. Appliquer le même méthode pour ne plus avoir de racine carrée au dénominateur dans les quotients suivant :
A= 6/ √3 + √5 Faut-il que j'ajoute √3 - √5 au numérateur et au dénominateur ?
B= 5/ -2 √3 Comme pour le A est-ce que je dois ajouté +2√3 ?
C= √6/ √2+ √3. J'ajoute √2 - √3 au numérateur et dénominateur ???
J'attend vos message. Merci par avance
J'ai un exercice à effectué mais je ne le comprend pas.
1. Vérifier par le calcul que (√5 - √2)(√5 + √2 ) est un nombre entier.
En tapant ce calcul sur ma calculatrice je trouve 3 et 3 est un nombre entier. Faut-il que je developpe ce calcul ?
2. Pour ne plus avoir de racine carrée au dénominateur de A= 1/√5- √2' , Chloé propose de multiplier le numérateur et le dénominateur par √5+√2. Effectuer ce calcul puis conclure.
Le dénominateur disparaît est on obtiens 7, 480025655 ???
3. Appliquer le même méthode pour ne plus avoir de racine carrée au dénominateur dans les quotients suivant :
A= 6/ √3 + √5 Faut-il que j'ajoute √3 - √5 au numérateur et au dénominateur ?
B= 5/ -2 √3 Comme pour le A est-ce que je dois ajouté +2√3 ?
C= √6/ √2+ √3. J'ajoute √2 - √3 au numérateur et dénominateur ???
J'attend vos message. Merci par avance
Re: La quantité conjuguée
Pour la première question, tu n'as pas besoin de calculatrice. Un papier un crayon, 2 lignes de calcul, résultat =3.
L'expression qu'on te demande de calculer , elle est de la forme (a-b)(a+b) en remplaçant a et b par ... et ...
Est-ce que (a-b)(a+b), ça te fait penser à quelque chose ?
L'expression qu'on te demande de calculer , elle est de la forme (a-b)(a+b) en remplaçant a et b par ... et ...
Est-ce que (a-b)(a+b), ça te fait penser à quelque chose ?
Re: La quantité conjuguée
Bonjour ;
1.
Ce serait bien si tu développes ton calcul en utilisant une identité remarquable :(a + b) = a^2 - b^2) .
.
Pour ton exercice , tu as :(\sqrt5+\sqrt2) = .....) .
.
1.
Ce serait bien si tu développes ton calcul en utilisant une identité remarquable :
Pour ton exercice , tu as :
Re: La quantité conjuguée
Pardon Lyceen95 , je n'avais pas vu ton message . Je te laisse continuer .
Re: La quantité conjuguée
donc si tu veux bien , tu peux faire le calcul pour passer aux autres questions .
Re: La quantité conjuguée
Ce n'est pas "et" mais "-" : 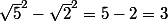 .
.
Pour continuer , on a :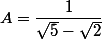 .
.
D'après Chloé , on a :(\sqrt5+\sqrt2)}}) .
.
Tu peux continuer maintenant : le dénominateur ne disparait pas , mais c'est le signe de racine carrée qui disparait du dénominateur .
Pour continuer , on a :
D'après Chloé , on a :
Tu peux continuer maintenant : le dénominateur ne disparait pas , mais c'est le signe de racine carrée qui disparait du dénominateur .
Re: La quantité conjuguée
D'accord
1/ √5- √2 = √5+√2/ (√5-√2)(√5+√2. On a donc :
√5+√2/ 5 au carré - 2 au carré ??
1/ √5- √2 = √5+√2/ (√5-√2)(√5+√2. On a donc :
√5+√2/ 5 au carré - 2 au carré ??
Re: La quantité conjuguée
Pour mon dernier exercice je doit appliquer la même méthode pour ne plus avoir de racine carrée au dénominateur dans les quotients suivants :
A= 6/ √3+√5 . A= 6/ √3+√5 = 6 √3-√5 ??
B= 5/2-√3. B= 5/2-√3= 5 2+√3 ??
C= √6/ √2+√3 C= √6/ √2+√3 = √6 + √2-√3 ??
A= 6/ √3+√5 . A= 6/ √3+√5 = 6 √3-√5 ??
B= 5/2-√3. B= 5/2-√3= 5 2+√3 ??
C= √6/ √2+√3 C= √6/ √2+√3 = √6 + √2-√3 ??
Re: La quantité conjuguée
B = 5/2-√3 = 5(2-√3)/ (2-√3)(2+√3) = 5(2-√3)/ √2 au carrée -√3 au carré
= 5(2-√3) / 4 - 9 = 5(2-√3) / -5 .
Est-ce correct ?
= 5(2-√3) / 4 - 9 = 5(2-√3) / -5 .
Est-ce correct ?
Re: La quantité conjuguée
Non .
B = 5/2-√3 = 5(2+√3)/ (2-√3)(2+√3) = 5(2+√3)/ 2 au carrée -√3 au carré
= 5(2+√3) / 4 - 3 = 5(2+√3).
B = 5/2-√3 = 5(2+√3)/ (2-√3)(2+√3) = 5(2+√3)/ 2 au carrée -√3 au carré
= 5(2+√3) / 4 - 3 = 5(2+√3).
Re: La quantité conjuguée
Et pour le D est-ce juste ?
D= √6/√2+√3. D= √6/√2+√3 = 6(√2-√3)/ (√2+√3)(√2-√3) = 6(√2-√3) / √2 au carrée -√3 au carrée
= √6(√2-√3) / 4 - 9 = √6(√2-√3)/ -5
D= √6/√2+√3. D= √6/√2+√3 = 6(√2-√3)/ (√2+√3)(√2-√3) = 6(√2-√3) / √2 au carrée -√3 au carrée
= √6(√2-√3) / 4 - 9 = √6(√2-√3)/ -5
Re: La quantité conjuguée
Tu refais la même faute pour (√3)² = 3 et non 9 et (√2)² = 2 et non 4 .
Etu45 a écrit:Et pour le D est-ce juste ?
D= √6/√2+√3. D= √6/√2+√3 = 6(√2-√3)/ (√2+√3)(√2-√3) = 6(√2-√3) / √2 au carrée -√3 au carrée
= √6(√2-√3) / 2 - 3 = √6(√2-√3)/- 1 = √6(√3-√2)
Modifié en dernier par aymanemaysae le 23 Oct 2019, 15:18, modifié 1 fois.
Re: La quantité conjuguée
Jusque la : D= √6/√2+√3. D= √6/√2+√3 = 6(√2-√3)/ (√2+√3)(√2-√3) = 6(√2-√3) / √2 au carrée -√3 au carrée . Est-ce correct ?
Je ne comprend pas mon erreur pouvais vous me l'expliquer ?
Je ne comprend pas mon erreur pouvais vous me l'expliquer ?
Re: La quantité conjuguée
Etu45 a écrit:Jusque la : D= √6/√2+√3. D= √6/√2+√3 = 6(√2-√3)/ (√2+√3)(√2-√3) = 6(√2-√3) / √2 au carrée -√3 au carrée . Est-ce correct ?
Je ne comprend pas mon erreur pouvais vous me l'expliquer ?
Jusqu'ici , c'est juste : l'erreur vient quand tu remplaces √2 au carrée par 4 et √3 au carrée par 9 ,
alors qu'il faut remplacer √2 au carrée par 2 et √3 au carrée par 3 .
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
