Bonjour,
0^0: ça existe? A-t-on 0^0=1?
0 puissance 0
11 messages
- Page 1 sur 1
Par convention, on pose 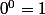 . C'est principalement pour des raisons de commodité, dans l'écriture des polynômes par exemple. Tu peux lire http://faq.maths.free.fr/html/node26.html pour plus de précisions
. C'est principalement pour des raisons de commodité, dans l'écriture des polynômes par exemple. Tu peux lire http://faq.maths.free.fr/html/node26.html pour plus de précisions
C'est une définition: dc c'est pas censé se démontré...
Cela étant, j'essaie qd meme:
Soit f la fonction de E ds R qui à tt x associe x^x.
E=la réunion de l'ensemble des entiers négatifs et de R+*
Alors lim(x->0)f(x)=0 (car pr tt x>0, f(x)=exp(ln(x)))
Si f est continue en 0, alors lim(x->0)f(x)=0=f(o) et c'est gagné.
Le tt est de mq que f est continue en 0...
Cela étant, j'essaie qd meme:
Soit f la fonction de E ds R qui à tt x associe x^x.
E=la réunion de l'ensemble des entiers négatifs et de R+*
Alors lim(x->0)f(x)=0 (car pr tt x>0, f(x)=exp(ln(x)))
Si f est continue en 0, alors lim(x->0)f(x)=0=f(o) et c'est gagné.
Le tt est de mq que f est continue en 0...
Dire que 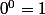 est une convention couramment utilisée et qui permet de prolonger par continuité la fonction
est une convention couramment utilisée et qui permet de prolonger par continuité la fonction 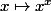 en
en  .
.
Ce n'est pas la seule convention possible cependant, et comme il n'existe pas de prolongement par continuité en) à la fonction de deux variables
à la fonction de deux variables \mapsto x^y) , on ne peut pas vraiment dire que poser
, on ne peut pas vraiment dire que poser 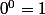 est naturel. Par exemple, si l'on voulait prolonger par continuité la fonction
est naturel. Par exemple, si l'on voulait prolonger par continuité la fonction  en
en  , on aurait plutôt tendance à poser
, on aurait plutôt tendance à poser  .
.
Bref, si l'on a à utiliser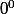 dans un calcul (ce qui n'arrive pas si souvent), il vaut mieux préciser la convention utilisée au lecteur.
dans un calcul (ce qui n'arrive pas si souvent), il vaut mieux préciser la convention utilisée au lecteur.
Ce n'est pas la seule convention possible cependant, et comme il n'existe pas de prolongement par continuité en
Bref, si l'on a à utiliser
khivapia a écrit:tout dépend de la branche des maths dans laquelle on se situe :
algèbre : 0^0=nbre d'applications de vide dans vide = 1 (l'application vide)
analyse : 0^0=e(0^ln(0) ) n'est défini
bonjour,
pas tout à fait d'accord. Les maths forment un tout : on ne peut avoir de conclusions différentes que si les axiomes de depart sont differents, comme le cas des geometries euclidienne et non euclidiennes. Le cas des nombres reels est une des applications de l'algébre et donc, il ne peut pas y avoir de difference avec l'analyse dans ce cas...
on peut quand même definir par continuité (comme cela a été déjà dit) et passage à la limite.
en analyse :
x^x=e(x*ln(x)) et lim(x*ln(x)) = 0 si x-->0
donc lim (x^x) = e^0 = 1 si x--> 0.
c'est comme pour sin(x)/x....
Non inscrit a écrit:ln(0)???!!
c'est un passage à la limite un peu hasardeux
cesar a tout à fait raison, je voulais juste souligner que ce n'est pas nécessairement une convention. Par exemple, la définition par prolongement de al fonction exp(x ln(x) ) est difficile si on se place sur Q, il n'est pas nécessaire de faire appel à la puissance de la construction de R pour être sûr que 0^0 = 1, c'est plutôt je dirais heureux que la théorie soit cohérente.
peut être ça parait logique ce que je vais dire.




Si on part pour travailler avec les limites, on aura +inf-inf qui est une forme indéterminée, peut être on peut la rendre une forme determinée. C'était la démonstration que j'ai faite quand la calculatrice m'a affiché "Error" en tentant de calculer . Peut être j'ai pas les outils qui me feront comprendre ce que vous avez fait, mais bon voilà.
. Peut être j'ai pas les outils qui me feront comprendre ce que vous avez fait, mais bon voilà.
Je pense que ça n'existe pas, mais comme certain on répondu que par convention, on prend égal à 1 (ce que je savais avant) ou à 0.
Et ce 0 pose toujours des problèmes.:doh:




Si on part pour travailler avec les limites, on aura +inf-inf qui est une forme indéterminée, peut être on peut la rendre une forme determinée. C'était la démonstration que j'ai faite quand la calculatrice m'a affiché "Error" en tentant de calculer
 . Peut être j'ai pas les outils qui me feront comprendre ce que vous avez fait, mais bon voilà.
. Peut être j'ai pas les outils qui me feront comprendre ce que vous avez fait, mais bon voilà.Je pense que ça n'existe pas, mais comme certain on répondu que par convention, on prend égal à 1 (ce que je savais avant) ou à 0.
Et ce 0 pose toujours des problèmes.:doh:
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
