Puissance 3/2 ??
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
iuddknd
- Messages: 7
- Enregistré le: 30 Aoû 2015, 19:30
-
 par iuddknd » 30 Aoû 2015, 21:12
par iuddknd » 30 Aoû 2015, 21:12
Bonsoir,
Je cherche à isoler z^2 dans :

Je ne vois pas du tout comment gérer la puissance 3/2.
En effet, 3/2 = 3 * 1^2
Faut il que je distribu la puissance 3 et la racine carrée dans ma parenthèse ?
Cordialement,

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2015, 21:17
par ampholyte » 30 Aoû 2015, 21:17
Bonjour,
Cela risque d'être un peu compliqué si tu veux développer.
Par contre ce que tu sais :
^{\frac{2}{3}} = x)
Il te suffit donc d'isoler le terme en (R² + z²)^(3/2) et d'appliquer à la puissance (2/3) l'ensemble de l'expression, tu n'auras plus qu'à soustraire par R² pour avoir exprimer z² en fonction du reste.
-
iuddknd
- Messages: 7
- Enregistré le: 30 Aoû 2015, 19:30
-
 par iuddknd » 30 Aoû 2015, 21:32
par iuddknd » 30 Aoû 2015, 21:32
ampholyte a écrit:Bonjour,
Cela risque d'être un peu compliqué si tu veux développer.
Par contre ce que tu sais :
^{\frac{2}{3}} = x)
Il te suffit donc d'isoler le terme en (R² + z²)^(3/2) et d'appliquer à la puissance (2/3) l'ensemble de l'expression, tu n'auras plus qu'à soustraire par R² pour avoir exprimer z² en fonction du reste.
Merci à toi ; comment l'idée d'utiliser
^{\frac{2}{3}} = x)
t'es venu ?
Je n'arrivé jamais à trouver les bonnes techniques dans quelque chose d'un peu plus technique qu'un calcul trivial ....

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2015, 22:02
par ampholyte » 30 Aoû 2015, 22:02
Bonjour,
Il faut penser à un exemple avec la racine carré. Soit a un réel quelconque alors :
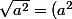^{\frac{1}{2}} = a)
La racine carré est en fait une puissance (1/2) ce qui "annule" la puissance de 2.
-
iuddknd
- Messages: 7
- Enregistré le: 30 Aoû 2015, 19:30
-
 par iuddknd » 30 Aoû 2015, 22:46
par iuddknd » 30 Aoû 2015, 22:46
ampholyte a écrit:Bonjour,
Il faut penser à un exemple avec la racine carré. Soit a un réel quelconque alors :
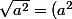^{\frac{1}{2}} = a)
La racine carré est en fait une puissance (1/2) ce qui "annule" la puissance de 2.
euh pour tout a positif non ?
car pour tout a :

même si je trouve bizarre que "la racine carré est en fait une puissance (1/2)" car la multiplication est commutative sur R et
^2)
est différent de


-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2015, 23:04
par ampholyte » 30 Aoû 2015, 23:04
iuddknd a écrit:euh pour tout a positif non ?
car pour tout a :

même si je trouve bizarre que "la racine carré est en fait une puissance (1/2)" car la multiplication est commutative sur R et
^2)
est différent de

Oui tout à fait pour a un réel quelconque positif je pensais l'avoir précisé dans mon post précédent mais non désolé pour cela =).

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Aoû 2015, 17:18
par zygomatique » 31 Aoû 2015, 17:18
iuddknd a écrit:Merci à toi ; comment l'idée d'utiliser
^{\frac{2}{3}} = x)
t'es venu ?
Je n'arrivé jamais à trouver les bonnes techniques dans quelque chose d'un peu plus technique qu'un calcul trivial ....
salut
puisque pour tout réel x ::

il suffit d'écrire

pour tout réel non nul a
...
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
 par tototo » 31 Aoû 2015, 17:33
par tototo » 31 Aoû 2015, 17:33
iuddknd a écrit:Bonsoir,
Je cherche à isoler z^2 dans :

Je ne vois pas du tout comment gérer la puissance 3/2.
En effet, 3/2 = 3 * 1^2
Faut il que je distribu la puissance 3 et la racine carrée dans ma parenthèse ?
Cordialement,
Bonjour
On pourra multiplier par 2/3 puis multiplier le denominateur puis multiplier le denominateur par B afin d'isoler z.
-
Black Jack
 par Black Jack » 01 Sep 2015, 11:59
par Black Jack » 01 Sep 2015, 11:59
(R²+z²)^(3/2) = µo.I.R²/(2B)
R²+z² = (µo.I.R²/(2B))^(2/3)
z² = (µo.I.R²/(2B))^(2/3) - R²
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités


est différent de
t'es venu ?
