Propriétés de la parabole [2de]

[Anonyme]

Bonjour,

Voici un nouvel exercice qui porte cette fois-ci sur la parabole.
Ci-dessous, l'énoncé ainsi que mes réponses aux questions posées.

Le plan est rapporté au repère orthonormal (O,i,j).
p étant un paramètre réel strictement positif, on note F le point de coordonnées (0,p/2) et (D) la droite d'équation y=-p/2.
1. Déterminez une équation de l'ensemble (P) des points équidistants de F et de (D). En déduire une définition géométrique de la parabole.
Remarque : F est appelé foyer de la parabole et D directrice de la parabole
Soit M(x;y) appartenant à (P). Appelons H le projeté orthogonal de M sur (D) [puisque l'on parle de distance à une droite]
Alors : H(x;-p/2) car H appartient à (D) donc vérifie l'équation de cette droite.
Nous savons que M appartient à P si et seulement si :
MF=HM
ssi MF²=HM²
ssi x²+(y-p/2)²=(y+p/2)² [On utilise la notion de distance entre deux points dans un repère orthonormal. Ici, je n'ai pas mis la racine carrée car les distances ont été élevées au carré.]
ssi x²+y²-py+p²/4=y²+py+p²./4

ssi x²=2py

Une équation de (P) est x²=2py.

2. (d) étant une droite donnée, montrez que les points d'intersection de (P) et (d) sont les centres, lorsqu'ils existent, des cercles tangents à (D) passant par F.
Soit K un point d'intersection de (P) et (d). Notons R son projeté orthogonal sur la droite (D).
K appartient à (P) donc KR=KF. Ceci signifie que R et F appartiennent au cercle de centre K. Notons C ce cercle. C est tangent à (D) en R car, comme R est le projeté orthogonal de K sur (D), on a nécessairement : (KR) et (D) sont perpendiculaires. On sait par ailleurs que K est le centre du cercle. On a donc prouvé que C est tangent à (D) en R. C passe par F. Nous avons donc démontré la propriété suivante : les points d'intersection de (P) et (d) sont les centres, lorsqu'ils existent, des cercles tangents à (D) passant par F.


Mes attentes : Mes réponses sont-elles correctes ? Pouvez par ailleurs m'aider à répondre à cette question :
3. Déterminez à partir de la question 2. l'ensemble des milieux de segments dont les extremités sont les points d'intersection (lorsque cette dernière est non vide) de (P) avec une famille de droites de direction fixe.
Dans un deuxième temps, vous retrouverez ce résultat par le calcul.
--> Je ne comprends pas ce qu'est une "famille de droites".

Merci d'avance !

PS : La question subsidiaire : Que pensez vous de cet exercice (difficulté, intérêt, préparation à la 1ère S...) ?

[Finrod]

les points d'intersection de (P) et (d) sont les centres, lorsqu'ils existent

le "lorsqu'il existent" est ambiguë dans l'énoncé. Il s'applique aux points d'intersection de (d) et (P) , (d) pouvant ne pas couper (P).
Les centres eux, considéré intrinsèquement, existent toujours.

Une famille de droite de direction fixe, c'est l'ensemble des droites ayant u même coefficient directeur.

Pour 0 par ex, c'est l'ensemble des droites horizontales.

[Anonyme]

Ma réponse est donc incomplète ?

[Anonyme]

erci pour ta réponse détaillée. Et bien pour la question 2., à priori, cet ensemble est une droite, je pense.
Maintenant, je ne vois pas trop comment aborder cette question...

[Finrod]

La famille de droite est d'équation y=ax+b et b varie. On cherche x en fonction de b.

Les deux points d'intersection vérifient aussi y=2px²

ça donne un trinôme du second degrés en x, ses racines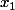 et 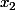donnent les abscisses des deux points solutions (quand ils existent) en fonction de b. Il reste à trouver les coordonnées.

Et enfin à calculer les coordonnées du milieu en fonction de b.

(ça à l'air de se simplifier)

[Anonyme]

Merci pour cette méthode analytique. Y aurait il une méthode plus géométrique qui s'appuierait sur ce qui a été démontré en 2. ?

[Anonyme]

Des idées ?