Produit de 3 vecteurs
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Zazou98
- Messages: 3
- Enregistré le: 03 Sep 2017, 15:50
-
 par Zazou98 » 03 Sep 2017, 15:59
par Zazou98 » 03 Sep 2017, 15:59
Bonjour, cela fait maintenant presque 2h que je suis bloqué sur cet exercice.
Je ne comprend pas comment trouve-t-on que cette multiplication de vecteur est égale à 7.
Quelqu'un pourrait m'aider?
 \vec{AC}:(-3;0;0) \vec{AD}:(-1;2;3))
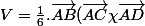 = 7)
Merci d'avance

Modifié en dernier par
Zazou98 le 03 Sep 2017, 16:04, modifié 1 fois.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 03 Sep 2017, 17:26
par Viko » 03 Sep 2017, 17:26
Il y a un probleme V est a la fois le produit d'un scalaire et d'un vecteur et simplement un scalaire, il doit y avoir une erreur qlq part
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 03 Sep 2017, 17:28
par zygomatique » 03 Sep 2017, 17:28
il est évident que cette écriture ne veut rien dire ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 03 Sep 2017, 17:51
par pascal16 » 03 Sep 2017, 17:51
(1/6) de AB scalaire (AC vectoriel AD) = 6
-
Zazou98
- Messages: 3
- Enregistré le: 03 Sep 2017, 15:50
-
 par Zazou98 » 03 Sep 2017, 18:11
par Zazou98 » 03 Sep 2017, 18:11
Il s'agit du calcul pour trouver le volume du tétraèdre ABCD.
Il est écris tel quel dans mon correctif. Connaissez vous un autre moyen de calculer son volume?
-
Zazou98
- Messages: 3
- Enregistré le: 03 Sep 2017, 15:50
-
 par Zazou98 » 03 Sep 2017, 20:01
par Zazou98 » 03 Sep 2017, 20:01
J'obtient egalement 6 en faisant le calcul du determinant. Ils ont du se tromper alors j'imagine.
Merci pour ta réponse

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités