Produit scalaire

[trtr]

voila j'ai des exercices auxquels je n'est rien compris sa serait vraiment sympa de m'aider. merci d'avance.deoler c'est un peu long.

exercice1:

1)determiner le centre et le rayon du cercle d'equation:
x²+y²-2x-2y-7=0
2)ce cercle coupe l'axe des abcisses en A et B et l'axe des ordonnees ( on nommera A le point dont l'abcisse est la plus petite)
3)determiner une equation du cercle de diametre [CD]
4)determiner une equation du cercle de centre A et passant par B.

exercice 2:

on donne les points d'equation A(3;1) et B(-3;3)

1) determiner une equation de la mediatrice de [AB] puis celle de [OB]
2) en deduire les coordonneees du point I centre du cercle circonscrit au triangle ABO.
3) determiner alors une equation du cercle circonscrit a ABO
4) determiner une equation de la tangente en B au cercle .

exercice 3:

soit A et B deux points distincts tels que AB=2.
on considere G le barycentre des points ponderes (A,3) et (B,1)

1)construire le point G . calculer GA et GB .
2)demontrer que pour tout point M du plan , on a:
3MA²+MB²=4MG² +3
3)determiner alors l'ensemble des points M du plan tels que:
3MA²+MB²=4
4) verifier alors que A appartient a to

[maf]

Exercice 1
1) le cercle peut s'écrire de manière suivante : soit M(xm;ym) le centre du cercle et r son rayon essaie de ré-écrire ton équation sous cette forme !

2) x=0 est l'équation de l'axe des abscisses y=0 est l'équation de l'axe des ordonnées remplace ces valeurs dans ton équation ! et trouve donc les points d'intersections

3) heu ... est-ce qu'on a des informations sur C et D ?

4) utilise la forme d'équation que je t'ai donnée sous 1)

[maf]

Exercice 2
1) L'équation d'une droite à la forme suivante : ici, X est le point milieu de AB, et ici : 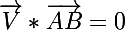essaye d'en resortir une équation cartésienne

2) L'intersection des médiatrices et le centre du cercle circonscrit

3) Utilise la forme 1) de l'exercice 1

4) Utilise la forme donne en 1) ... avec X est le point B et puisque la tangente est perpendiculaire au rayon

[trtr]

tu pourrait me dire comment faire plus precisement s'il te plait , les deux premiers exercices et j'essairai comme sa de faire le troisieme . sa serait vraiment sympa

[trtr]

s'il vous plait...

[trtr]

oui mais pour tout dire je men rappele plus trop

[trtr]

s'il te plait ... j'y arrive pas , je demanderai pas si j'etais pas pommer ...

[trtr]

............

[trtr]

........ je vous en supplit

[trtr]

s'il vous plait s'est vraiment important

[trtr]

je vous en supplit ....