bonsoir je n'arrive pas cet exercice :
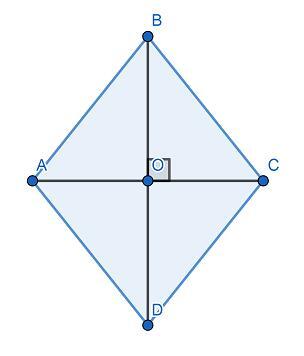
ABCD est un losange tel que AC = 8 et BD =10.
On note O le centre de ce losange.
1. a. En introduisant le point O, calculer AB au carré.
b. En déduire la longueur AB.
2. Calculer les produits scalaires suivants.
a. AC . BD ; BC . BD ; AB . AC
b. AO . AD ; AB . DC ; DB . OC.
mon brouillon :
1.
a. Le centre O divise les diagonales AC et BD en deux segments de longueurs égales, donc AO = OB = 1/2 * AC = 1/2 * 8 = 4.
Dans le triangle rectangle AOB, on peut utiliser le théorème de Pythagore :
AB^2 = AO^2 + OB^2
AB^2 = 4^2 + 4^2
AB^2 = 16 + 16
AB^2 = 32
b. En prenant la racine carrée des deux côtés, on obtient :
AB = racine carré de 32 = 4 racine carré de 2
2.
a) Calcul des produits scalaires :
AC . BD : Comme les diagonales d'un losange se croisent à angle droit, les vecteurs AC et BD sont perpendiculaires. Donc, leur produit scalaire est nul.
AC . BD = 0
BC . BD : Les vecteurs BC et BD ont la même direction, donc le produit scalaire sera égal au carré de la norme de BD.
BC . BD = ||BD||^2 = 10^2 = 100
AB . AC: Les vecteurs AB et AC ont la même direction, donc le produit scalaire sera égal au carré de la norme de AB.
AB . AC = ||AB||^2 = 32
b) Calcul des produits scalaires :
AO . AD : Les vecteurs AO et AD ont la même direction, donc le produit scalaire sera égal au carré de la norme de AO.
AO . AD = ||AO||^2 = 4^2 = 16
AB . DB : Comme AB et DB sont des côtés opposés d'un losange, ils sont perpendiculaires, donc leur produit scalaire est nul.
AB . DB = 0
DB . OC : Comme DB et OC sont des côtés opposés d'un losange, ils sont perpendiculaires, donc leur produit scalaire est nul.
DB . OC = 0
merci tout le monde
Produit scalaire
9 messages
- Page 1 sur 1
Re: produit scalaire
Bonjour, il faut revoir le début
En restant sur le thème (produit scalaire et introduction de O) on peut aussi écrire
}^2={\vec{AO}}^2+{\vec{OB}}^2)
car les vecteurs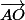 et
et 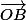 sont orthogonaux...
sont orthogonaux...
sarahdvz66 a écrit:bonsoir je n'arrive pas cet exercice :
ABCD est un losange tel que AC = 8 et BD =10.
On note O le centre de ce losange.
1. a. En introduisant le point O, calculer AB au carré.
mon brouillon :
1.
a. Le centre O divise les diagonales AC et BD en deux segments de longueurs égales, donc AO = OB = 1/2 * AC = 1/2 * 8 = 4.
Non AO=OC = 8 et OB=OB=10/2=5
En restant sur le thème (produit scalaire et introduction de O) on peut aussi écrire
car les vecteurs
Re: produit scalaire
Bonjour, il faut revoir le début
En restant sur le thème (produit scalaire) on peut aussi écrire
}^2={\vec{AO}}^2+{\vec{OB}}^2)
car les vecteurs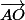 et
et 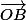 sont orthogonaux...
sont orthogonaux...
sarahdvz66 a écrit:bonsoir je n'arrive pas cet exercice :
ABCD est un losange tel que AC = 8 et BD =10.
On note O le centre de ce losange.
1. a. En introduisant le point O, calculer AB au carré.
mon brouillon :
1.
a. Le centre O divise les diagonales AC et BD en deux segments de longueurs égales, donc AO = OB = 1/2 * AC = 1/2 * 8 = 4.
Non AO=OC = 4 et OB=OB=10/2=5
En restant sur le thème (produit scalaire) on peut aussi écrire
car les vecteurs
Re: produit scalaire
non, je ne comprends rien pour calculer les produits scalaires, sachant que c’est pour demain 8h et que je sais maintenant que j’ai faux..
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :