Produit scalaire

[nali]

Bonjour,
J'ai un exo où je coince sur le calcul d'un produit scalaire dans un triangle ABC.
On a A(0;3) B(2;-1) C(-2;3) et H(x;y) qui correspond à l'orthocentre (croisement des hauteurs).
Je dois calculer de 2 façons le produit scalaire de AH.CB

Par la méthode des coordonnées, je trouve AH.BC=4(x-y+3)
Je sais aussi que ce résultat est égal à zéro puisqu'il s'agit du produit d'une base par sa hauteur(et qu'il donne l'équation de la hauteur).

Par contre, la seconde méthode me pose souci:
Si j'utilise la méthode avec l'angle, comme cos90° fait zéro, j'obtiens un résultat nul (donc sans x ou y).
Si j'utilise la formule u.v=u²+v²-(u-v)² (il s'agit des normes), même chose, je trouve zéro puisque tout s'annule.
Cette formule semblait être pourtant la plus prometteuse puisqu'après j'aurais utilisé les distances.
Avec les projetés, même chose puisque il s'agit de droites perpendiculaires.
Auriez-vous une idée?

[Carpate]

Bonsoir,

Par contre, la seconde méthode me pose souci:
Si j'utilise la méthode avec l'angle, comme cos90° fait zéro, j'obtiens un résultat nul (donc sans x ou y).
Si j'utilise la formule u.v=u²+v²-(u-v)² (il s'agit des normes), même chose, je trouve zéro puisque tout s'annule.
Cette formule semblait être pourtant la plus prometteuse puisqu'après j'aurais utilisé les distances.

Ce n'est pas très clair.
S'il s'agit de calculer les coordonnées de l'orthocentre du triangle :
- un premier produit scalaire nul :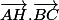 donne une équation de la hauteur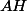
- un deuxième par exemple donne une équation de la hauteur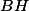
Et il n'y a plus qu'à calculer l'intersection de ces 2 droites ...

[nali]

Je répète:
Je dois calculer de 2 façons le produit scalaire de AH.CB
J'ai fait d'une façon avec les coordonnées....je ne trouve pas la seconde façon qui me permettrait de retomber sur le même résultat que la première façon.
C'est plus clair?

[Carpate]

Et si donnais l'énoncé complet ?

[nali]

On considère A(0;3), B(2;-1) et C(-2;3) trois points du plan.
On cherche à déterminer les coordonnées du point H(x;y), orthocentre du triangle ABC.
1)a)Calculer de 2 façons le produit scalaire AH.CB
Voilà, c'est tout, j'avais déjà tout indiqué au début de ma question.

[GaBuZoMeu]

Tu l'as déjà calculé de deux façons : une façon en l'exprimant en fonction des coordonnées x et y de H, une autre façon en remarquant que, par définition de l'orthocentre, est orthogonal à .