Produit scalaire

[Leika]

J'ai résolu l’équation et j'obtient 4x-8y-12=0, ensuite quand on divise tout par 4 j'obtient x-2y-3=0 mais comment rédigé ?
et pour la derniere question il faut la mettre sous qu'elle forme ?
merci :)

[Rizmoth]

Eh bien voilà, tu détailles correctement la résolution du système, et tu n'as plus qu'à faire une phrase de conclusion :
"Les coordonnées (x;y) du point M vérifient donc bien l'équation x - 2y + 3 = 0."

La question 4 est presque superflue...je ne vois vraiment pas ce qu'il y a à ajouter. Si on veut être vraiment précis (quitte à se répéter), on dira :
"La droite (IM) a pour équation cartésienne x - 2y + 3 = 0. Or cette droite est confondue avec la médiatrice du segment [AB].
Donc a fortiori, la médiatrice du segment [AB] a pour équation x - 2y + 3 = 0."

[Leika]

merciiii beaucoup

[mathelot]

rédaction:



cet ensemble de points est formé de points du plan
situés sur une perpendiculaire à (AB)

- comme I appartient à (D) (on fait M=I)
- comme le produit scalaire donne une équation d'une droite (D)
- comme D est perpendiculaire à (AB)
- comme x-2y+3=0 est l'équation d'une droite

alors une équation de la médiatrice de AB est
x-2y+3=0

sinon , pour rédiger , écrire des équivalences si le terme "équivalence" est employé dans ton lycée.

[Carpate]

Bien que l'exercice t'aiguille sur la voie du produit scalaire, tu aurais tout à fait le droit de proposer une autre solution (que tu peux proposer en "bonus") :
C.n.s pour que M(x,y) appartienne à la médiatrice de [AB] : soit : . Les termes en et 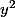ont le bon goût de disparaître et l'on retrouve l'équation recherchée ...

[mathelot]