Le produit scalaire dans la vie courante

[kygerard]

je souhaite avoir des images et figures de la vie courante qui traduise le produit scalaire dans le plan et dans l'espace pour le lycée

[LB2]

Bonjour kygerard,

le produit scalaire a été introduit en physique au XIX è siècle pour calculer le travail d'une force.

Intuitivement, quand une force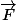 s'applique à un objet en mouvement avec un vecteur vitesse , le travail de la force 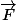est . Seule la composante de la force qui est dans la direction du mouvement travaille. Ce travail peut être moteur si elle est dans le sens du mouvement, ou résistance si elle est dans le sens inverse. La composante perpendiculaire ne travaille pas.
En général donc le travail est le produit des normes des vecteurs, multiplié par le cosinus de l'angle orienté. On retrouve bien le produit scalaire.

Exemple si tu veux pousser une voiture (moteur éteint) dans le sens de la route.
Si tu pousses dans le sens de la route : toute la force que tu appliques est utilisée pour le mouvement : angle nul, cosinus = 1
Si tu pousses dans le sens opposé à la route : toute la force que tu appliques est utilisée pour s'opposer au mouvement : angle = 180 °, cosinus = -1
Si tu pousses perpendiculaire au sens de la route :la force ne travaille pas, elle ne servira à rien pour avancer : angle 90°, cosinus = 0


Cordialement

[Pseuda]

Bonjour,

Dans l'espace, c'est pareil que dans le plan, car deux vecteurs sont toujours coplanaires, et que le cosinus de l'angle ne fait pas intervenir l'orientation.

Autrement dit, dans l'espace, le produit scalaire de deux vecteurs est toujours considéré dans le plan formé par les vecteurs.