Bonjour, je suis nouveau sur le forum. Pouvez-vous m'aider à la résolution de ce problème?
Un fermier décide de clôturer une partie rectangulaire de son jardin pour en faire un poulailler. Il dispose de 60m de treillis. Quels sont les dimensions qu'il doit donner à son poulailler pour que sa superficie soit la plus grande possible, dans le cas où le poulailler est adossé à un mur? ( le treillis sert donc à clôturer 3 cotés )
Merci d'avance pour votre aide
Problème
11 messages
- Page 1 sur 1
Re: Problème
Bonjour,
Comme toujours dans un problème commencer ainsi, il faut utiliser les indications de l'énoncé pour les transformer en relations mathématiques. En particulier, il faut identifier les inconnues qu'on va chercher.
On veut un poulailler rectangulaire : quelles sont alors les inconnues ? Et "grand classique" : faire un dessin en positionnant ces inconnues !
Avec ces inconnues, quelle est la formule pour le périmètre ? La formule pour l'aire ?
Sachant qu'on a 60m de treillis : est-ce que ces 60m vont servir pour l'aire ? pour le périmètre ? Avec la réponse à cette question, comment modifier l'une des formules précédentes ?
Enfin, on cherche l'aire maximale : cela fait penser à la recherche du maximum d'une fonction, ladite fonction étant l'aire. Pas de chance, si on ne s'est pas trompé, il y a 2 variables dans la formule de l'aire.
Mais ne peut-on pas utiliser la première formule pour donner une relation entre les deux variables, donc pour remplacer une des variables par cette relation dans le calcul de l'aire ?
Comme toujours dans un problème commencer ainsi, il faut utiliser les indications de l'énoncé pour les transformer en relations mathématiques. En particulier, il faut identifier les inconnues qu'on va chercher.
On veut un poulailler rectangulaire : quelles sont alors les inconnues ? Et "grand classique" : faire un dessin en positionnant ces inconnues !
Avec ces inconnues, quelle est la formule pour le périmètre ? La formule pour l'aire ?
Sachant qu'on a 60m de treillis : est-ce que ces 60m vont servir pour l'aire ? pour le périmètre ? Avec la réponse à cette question, comment modifier l'une des formules précédentes ?
Enfin, on cherche l'aire maximale : cela fait penser à la recherche du maximum d'une fonction, ladite fonction étant l'aire. Pas de chance, si on ne s'est pas trompé, il y a 2 variables dans la formule de l'aire.
Mais ne peut-on pas utiliser la première formule pour donner une relation entre les deux variables, donc pour remplacer une des variables par cette relation dans le calcul de l'aire ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Problème
Avez-vous fait un dessin ?
Tracez un rectangle. Il y a 4 côtés. Mais combien de côtés sont potentiellement différents en terme de longueur ?
Donnez un nom à chacun de ces côtés "différents". Quel est alors le périmètre du rectangle ? L'aire du rectangle ?
Je vous donnerai des indications après la réponse à ces deux questions. Si vous ne l'avez pas fait, faites le dessin et portez sur ce dessin les différents noms de longueur. Indiquez également sur le dessin où se trouve le mur.
Tracez un rectangle. Il y a 4 côtés. Mais combien de côtés sont potentiellement différents en terme de longueur ?
Donnez un nom à chacun de ces côtés "différents". Quel est alors le périmètre du rectangle ? L'aire du rectangle ?
Je vous donnerai des indications après la réponse à ces deux questions. Si vous ne l'avez pas fait, faites le dessin et portez sur ce dessin les différents noms de longueur. Indiquez également sur le dessin où se trouve le mur.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Problème
Il y a 4 côtés mais il y en a que 2 qui sont différents en terme de longueur. Si je devais nommer ces 2 côtés je les nommerais x et y. Donc à partir de x et y, les calculs de l'aire et du périmètre serait pour le périmètre:
2(x+y) et pour l'aire: x*y
Et oui j'ai fait mon dessin
2(x+y) et pour l'aire: x*y
Et oui j'ai fait mon dessin
Re: Problème
Ok, donc votre dessin doit ressembler à cela.







Puisque le périmètre est) , et sachant qu'on va utiliser 60m de treillis, comment va-t-on relier le périmètre avec ces 60m, sachant qu'on ne met pas de treillis côté mur ? (il faut trouver une égalité dans laquelle vont apparaitre des
, et sachant qu'on va utiliser 60m de treillis, comment va-t-on relier le périmètre avec ces 60m, sachant qu'on ne met pas de treillis côté mur ? (il faut trouver une égalité dans laquelle vont apparaitre des  , des
, des  et des 60)
et des 60)
Dès que vous avez cette égalité, utilisez-là pour exprimer en fonction de
en fonction de  (c'est-à-dire, une égalité de la forme
(c'est-à-dire, une égalité de la forme ) où
où ) est une formule ne contenant plus de
est une formule ne contenant plus de  )
)
Puisque le périmètre est
Dès que vous avez cette égalité, utilisez-là pour exprimer
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Problème
Sachant qu'en utilisant l'équation 2(x+y)on comprend le mur dans l'équation, alors je dirais que celle-ci vaut 2(x+y)=60+x (x étant le mur car il n'est pas compris dans les 60 mètres de treillis)
Après je diviserais le tout par 2 pour avoir le y tout seul ce qui donnerais x+y=30+x/2 et par après cela donnerais y=30+(x/2)-x
Suis-je sur la bonne voie?
Après je diviserais le tout par 2 pour avoir le y tout seul ce qui donnerais x+y=30+x/2 et par après cela donnerais y=30+(x/2)-x
Suis-je sur la bonne voie?
Re: Problème
Bonjour, Je me permets de prendre le relais. Oui c'est ça mais cela ne correspond pas au dessin de hdci. Le mur c'est y.
Ainsi d'après le dessin 60 = 2 x + y donc y=60-2 x
C'est pas faux ce que tu as fais mais tu échanges les rôles de x et y. Autant rester sur les notations de la figure.
Ainsi d'après le dessin 60 = 2 x + y donc y=60-2 x
C'est pas faux ce que tu as fais mais tu échanges les rôles de x et y. Autant rester sur les notations de la figure.
Re: Problème
(Ceci dit, si votre dessin avait placé  sur la longueur du mur, comme dit aviateur c'est correct : ici tout n'est question que de notations ; si vous le souhaitez, pour vous entraîner à manipuler les formules algébriques, vous pouvez tenter de résoudre ce problème avec la convention de mon dessin, ou la convention de votre dessin, et vérifier qu'on trouve bien la même chose).
sur la longueur du mur, comme dit aviateur c'est correct : ici tout n'est question que de notations ; si vous le souhaitez, pour vous entraîner à manipuler les formules algébriques, vous pouvez tenter de résoudre ce problème avec la convention de mon dessin, ou la convention de votre dessin, et vérifier qu'on trouve bien la même chose).
Avec [convention hdci] on a bien comme dit aviateur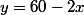
avec [convention LIVIOB] on a bien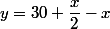 , mais ici il faut simplifier cette écriture car
, mais ici il faut simplifier cette écriture car 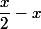 peut se simplifier.
peut se simplifier.
Notez bien que les deux écritures n'ont rien à voir l'une avec l'autre car ce ne sont pas les mêmes et les mêmes
et les mêmes  .
.
Dans les deux cas, une fois que vous avez) , pouvez-vous utiliser cela dans la formule de l'aire
, pouvez-vous utiliser cela dans la formule de l'aire 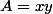 pour "faire disparaître
pour "faire disparaître  " en ne conservant que des
" en ne conservant que des  ? (A ce moment-là,
? (A ce moment-là,  devient en fait une fonction de x et on peut l'écrire
devient en fait une fonction de x et on peut l'écrire =\cdots) )
)
Avec [convention hdci] on a bien comme dit aviateur
avec [convention LIVIOB] on a bien
Notez bien que les deux écritures n'ont rien à voir l'une avec l'autre car ce ne sont pas les mêmes
Dans les deux cas, une fois que vous avez
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Problème
Oui c'est vrai mais il y a encore plus simple. Imaginons que le x et le y soient inversées sur le graphique(ce qui reviendrais au même), alors l'équation serait 2(x+y)=60+x
Si on transforme cette équation, ça ressemblerais plutôt à 2x+2y=60+x et par après 2y=60+x-2x et donc y=30-x/2
Après ça, j'ai donné des valeurs à x et y et j'ai trouvé plusieurs solutions: [si x=5 alors y=27,5][si x=10 alors y=25][si x=20 alors y=20][si x=30 alors y=15][si x=40 alors y=10][si x=50 alors y=5]et bien d'autres…
Après ça, j'ai fait un graphique de x en fonction de l'air et j'ai eu une parabole avec comme sommet(maximum) une aire de 450 pour x=30 et y=15
En tout cas merci beaucoup pour votre aide car vous m'avez aidé à trouvé l'équation
Sauriez-vous où trouver des problèmes similaires à celui-ci pour m'exercer ? Merci!
Si on transforme cette équation, ça ressemblerais plutôt à 2x+2y=60+x et par après 2y=60+x-2x et donc y=30-x/2
Après ça, j'ai donné des valeurs à x et y et j'ai trouvé plusieurs solutions: [si x=5 alors y=27,5][si x=10 alors y=25][si x=20 alors y=20][si x=30 alors y=15][si x=40 alors y=10][si x=50 alors y=5]et bien d'autres…
Après ça, j'ai fait un graphique de x en fonction de l'air et j'ai eu une parabole avec comme sommet(maximum) une aire de 450 pour x=30 et y=15
En tout cas merci beaucoup pour votre aide car vous m'avez aidé à trouvé l'équation
Sauriez-vous où trouver des problèmes similaires à celui-ci pour m'exercer ? Merci!
Re: Problème
C'est bien de "voir avec des exemples", mais un exemple n'est pas suffisant pour démontrer une valeur.
Vous avez "lu" le résultat sur une parabole, c'est effectivement bien une parabole, mais votre lecture est nécessairement imprécise : êtes-vous sûr que c'est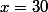 , et pas
, et pas 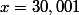 ?
?
La lecture graphique ne vous permet pas d'avoir ce niveau de précision.
Et dans un contrôle de mathématiques, ce raisonnement sera considéré comme faux (peut-être partiellement faux) par votre professeur de maths.
Je conviens toutefois que dans le cas de la construction du poulailler, un écart de 1mm sera vraiment le cadet des soucis du fermier ! Mais s'il ne s'agissait pas d'un poulailler, mais d'une centrale nucléaire, cette imprécision pourrait faire la différence entre un truc qui marche bien et une grosse catastrophe.
Revenons à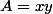 : avec votre convention et
: avec votre convention et 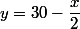 , on peut remplacer
, on peut remplacer  par
par 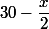 dans la formule de l'aire, et on obtient
dans la formule de l'aire, et on obtient
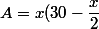=30x-\dfrac{x^2}{2})
Ainsi, A est bien un polynôme du second degré en x, et la courbe est bien une parabole. La parabole est orientée "vers le bas" (donc la fonction admet un maximum) car le signe devant est négatif.
est négatif.
Il y a plusieurs moyens de trouver le sommet, le plus rapide étant la formule suivante :
Ici,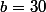 et
et 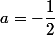 , l'abscisse du sommet est donc
, l'abscisse du sommet est donc 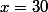
Pour trouver d'autres problèmes de mise en équation : vous pouvez chercher sur google avec les mots-clés "problèmes de mise en équation niveau lycée". En particulier, vous tomberez sur ce site
https://pedagogie.ac-reims.fr/index.php/maths-lycee/enseigner-maths-lycee/item/3466-problemes-mise-en-equation-resolution qui contient un document DOC avec l'énoncé de différents problème.
Je vous propose également celui-là :
Une brique pèse 2 kg et une demi-brique. Combien pèse la brique ?
Vous avez "lu" le résultat sur une parabole, c'est effectivement bien une parabole, mais votre lecture est nécessairement imprécise : êtes-vous sûr que c'est
La lecture graphique ne vous permet pas d'avoir ce niveau de précision.
Et dans un contrôle de mathématiques, ce raisonnement sera considéré comme faux (peut-être partiellement faux) par votre professeur de maths.
Je conviens toutefois que dans le cas de la construction du poulailler, un écart de 1mm sera vraiment le cadet des soucis du fermier ! Mais s'il ne s'agissait pas d'un poulailler, mais d'une centrale nucléaire, cette imprécision pourrait faire la différence entre un truc qui marche bien et une grosse catastrophe.
Revenons à
Ainsi, A est bien un polynôme du second degré en x, et la courbe est bien une parabole. La parabole est orientée "vers le bas" (donc la fonction admet un maximum) car le signe devant
Il y a plusieurs moyens de trouver le sommet, le plus rapide étant la formule suivante :
- dans
Ici,
Pour trouver d'autres problèmes de mise en équation : vous pouvez chercher sur google avec les mots-clés "problèmes de mise en équation niveau lycée". En particulier, vous tomberez sur ce site
https://pedagogie.ac-reims.fr/index.php/maths-lycee/enseigner-maths-lycee/item/3466-problemes-mise-en-equation-resolution qui contient un document DOC avec l'énoncé de différents problème.
Je vous propose également celui-là :
Une brique pèse 2 kg et une demi-brique. Combien pèse la brique ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
