Problème pour demain

[Gmma]

Bonjour

Svp aidez moi je n'y arrive pas du tout. Voici l'énoncé:
Un jardinier doit construire un parterre de fleurs ayant la forme d'un secteur circulaire de rayon x ( en mètres). Il dispose de 40 m de cloture pour l'entourer.

http://www.servimg.com/image_preview.php?i=1&u=11002824
1-calculez l'aire f(x) de ce secteur
2-Déterminez x pour que l'aire de ce secteur soit maximale.
3-Déterminez la valeur de l'angle correspondant.

Je ne comprend vraiment pas cet exercice.

Merci d'avance

[maturin]

là ton dessin ressemble plus à un triangle + un cercle qu'à un arc de cercle.
Un arc de cercle c'est une part de camembert

Donc pour calculer l'aire d'un arc de cercle tu calcules l'aire d'un cercle et tu applique une règle de trois pour dire
un arc de cercle d'angle 2pi représente l'aire totale du cercle (pi*r²)
donc un arc de cercle d'angle a représente ???

le périmètre total c'est 1 rayon + 1 rayon + un arc de cercle dont tu trouve la longueur de la même façon qu'avant (longueur d'un cercle = 2pir donc longueur d'un arc=???)
Tu va donc avoir une relation entre ton angle et x grace au périmètre = 40m

Si tu remplace cet angle dans l'expression de l'aire il ne te restera plus que des x.

2 - c'est un étude de fonction toute bête avec calcul de la dérivée, tableau de variation ....
3 - quand t'as x tu trouve l'angle grace à ta relation vue en 1.

[Gmma]

Alors voilà ce que j'ai trouvé

f(x)=20x-x².

Mais pour la suite??
POuvez vous m'aider s'il vous plaît??? :cry:

[rene38]

Bonsoir

Alors voilà ce que j'ai trouvé f(x)=20x-x².
Mais pour la suite ?

Exact. C'est pourtant très simple à dériver.

[maturin]

ben la suite c'est une étude de fonction.

ta fonction étant un polynome du second degré tu devrais savoir faire.

[Gmma]

je ne comprends vraiment pas comment on trouve la réponse du 1).
Pourriez vous me réexpliquer?



1) La longueur de l' arc est 40-2x.

L' aire d' un secteur angulaire est proportionnelle à la longueur de l' arc.

L' aire d' un disque de rayon x est pi x²; c' est un secteur angulaire particulier dont la longueur de l' arc est 2 pi x.

Pour traduire la proportionnalité, on écrit
A/(40-2x)=(pi x²)/(2 pi x) A étant l'aire du secteur.

donc A=(pi x²(40-2x))/(2 pi x)=(40 pi x²-2x^3)/ (2 pi x)

on simplifie donc A=20x-x².

Donc 1) f(x)=20x-x².

f(x) est nécessairement positif (une aire).

2) x appartient à [0;20].

f'(x)=-2x+20.
On résout cette équation x=10.

Tableau de variation
f croissante sur [0;10] et décroissante sur [10;20].

f admet un maximum pour x=10.
Il correspond à l'aire maximale du secteur f(10)=100.

Merci d'avance.

[Gmma]

Pourriez vous me réexpliquer la première question s'il vous plaît?
Je ne comprends pas comment on trouve f(x)=20x-x².

[maturin]

ben c'est toi qui l'a donné la formule donc on pensait que t'avais compris.

Alors tu écris:
soit l'angle de ton arc

un cercle (=arc d'angle ) a une longueur
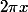
donc si tu n'as qu'un arc d'angle par une règle de trois tu trouves la longueur de l'arc égale à

ta longueur totale est de 40 donc tu as

L'aire d'un cercle (=camembert d'angle ) est de
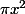
Donc l'aire de ton arc (camembert d'angle ) est de


donc tu as
hors =>

Donc

[Gmma]

Ca y est j'ai compris :id:
Merci de m'avoir réexpliquer.