Problème ouvert

par **lywet** » 02 Jan 2015, 17:05

bonjour, je suis élève de première S. Notre professeur de mathématiques nous a donné un problème ouvert pendant les vacances, mais je n'arrive pas à le résoudre.

Voila le problème:
On considère la parabole P d'équation y=x²
A et B sont deux points distincts de cette parabole. C est un point du segment [AB].
D est le point de P ayant la même abscisse que C

Déterminer la position du point C en fonction de celles de A et B pour que la distance CD soit maximale.

J'ai déjà trouvé que la distance CD était maximale quand C se trouvait au milieu de [AB] mais je n'ai aucune idée de comment le démontrer.
Merci d'avance pour votre aide,
Lywet

par **Carpate** » 02 Jan 2015, 17:43

lywet a écrit:bonjour, je suis élève de première S. Notre professeur de mathématiques nous a donné un problème ouvert pendant les vacances, mais je n'arrive pas à le résoudre.

Voila le problème:
On considère la parabole P d'équation y=x²
A et B sont deux points distincts de cette parabole. C est un point du segment [AB].
D est le point de P ayant la même abscisse que C

Déterminer la position du point C en fonction de celles de A et B pour que la distance CD soit maximale.

J'ai déjà trouvé que la distance CD était maximale quand C se trouvait au milieu de [AB] mais je n'ai aucune idée de comment le démontrer.
Merci d'avance pour votre aide,
Lywet

Tu pourrais établir l'équation de la droite (AB) avec

et

puis prendre un point C d'abscisse

appartenant à cette droite et établir les coordonnées de D puis la distance CD

par **lywet** » 02 Jan 2015, 19:44

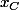
Carpate a écrit:Tu pourrais établir l'équation de la droite (AB) avec et puis prendre un point C d'abscisse appartenant à cette droite et établir les coordonnées de D puis la distance CD

Grace à votre conseil, j'ai pu trouver:

A (xa;xa²)
B (xb,xb²)

Équation de la droite (AB):
y=(xb+xa) x (x-xax xb)

Les coordonnées de C en fonction de y sont donc:
y=(xb+xa) x (xc-xa x xb)

Les coordonnées du point D sont: D(xd;xd²)

la distance CD est donc
CD= racine carrée de (xd-xc)²+(xd²-xc²)²

par contre ici je bloque.. je sais que je devrai arriver à un polynôme du second degré pour trouver alpha et beta, mais je ne sais pas comment le trouver
merci encore,
Lywet

par **zygomatique** » 02 Jan 2015, 19:51

salut

pourquoi t'embêter avec une racine carrée ...

CD est positif donc maximal lorsque son carré l'est ....

pourquoi compliquer les notations inutilement ....

il nous faut donc calculer y

or

donc ...

par **BiancoAngelo** » 02 Jan 2015, 19:51

lywet a écrit:Grace à votre conseil, j'ai pu trouver:

A (xa;xa²)
B (xb,xb²)

Équation de la droite (AB):
y=(xb+xa) x (x-xax xb)

Les coordonnées de C en fonction de y sont donc:
y=(xb+xa) x (xc-xa x xb)

Les coordonnées du point D sont: D(xd;xd²)

la distance CD est donc
CD= racine carrée de (xd-xc)²+(xd²-xc²)²

par contre ici je bloque.. je sais que je devrai arriver à un polynôme du second degré pour trouver alpha et beta, mais je ne sais pas comment le trouver
merci encore,
Lywet

L'équation de droite est tout sauf compréhensible...
Si tu n'écris pas en latex, peux-tu au moins utiliser "*" pour fois ?

Sinon, on discerne pas le x de l'opérateur "multiplication"...

Merci

Sinon, quand tu as l'équation de la droite, tu as un point C dessus, et donc tu as les coordonnées de C, tu prends (x,y) sachant que le y est donné par ton éq de droite.

Et n'oublie pas que

par **zygomatique** » 02 Jan 2015, 20:01

voir mon post au dessus ...

et trivialement l'équation de la droite (AB) est y = (a + b)(x - a) + a² y = (a + b)x - ab

et voir aussi http://www.ilemaths.net/forum-sujet-627689.html

par **BiancoAngelo** » 02 Jan 2015, 20:06

zygomatique a écrit:voir mon post au dessus ...

et trivialement l'équation de la droite (AB) est y = (a + b)(x - a) + a² y = (a + b)x - ab

et voir aussi http://www.ilemaths.net/forum-sujet-627689.html

Oui mais ce n'est pas à toi que je demandais de le faire, je sais bien que tu sais écrire en LATEX et faire des équations :lol3:

par **zygomatique** » 02 Jan 2015, 20:12

je sais ... mais il l'avait presque trouvée ...

je voulais aussi montrer qu'avec des notations simples tout devient plus lisible ... et ne nécessite même pas LaTeX ...

par **lywet** » 02 Jan 2015, 20:12

oui pas de problème :)

l'équation de AB est donc:
y=(xb+xa)x - xaxb

les coordonnées de c sont donc

y=(xb+xa)xc - xaxb

D (xc,xd²)

distance CD:
CD=(xc-xc)²+(xc²-xc²)² ?

par **BiancoAngelo** » 02 Jan 2015, 20:47

zygomatique a écrit:je sais ... mais il l'avait presque trouvée ...

je voulais aussi montrer qu'avec des notations simples tout devient plus lisible ... et ne nécessite même pas LaTeX ...

Ca roule, et je suis d'accord, pas toujours utile

par **BiancoAngelo** » 02 Jan 2015, 20:48

lywet a écrit:oui pas de problème

l'équation de AB est donc:
y=(xb+xa)x - xaxb

les coordonnées de c sont donc

y=(xb+xa)xc - xaxb

D (xc,xd²)

distance CD:
CD=(xc-xc)²+(xc²-xc²)² ?

Il faut écrire CD²=(xc-xc)²+(xd²-yc)²

par **lywet** » 02 Jan 2015, 21:24

d accord, je vois mon erreur.
mais du coup (xc-xc)² cela fait 0, il ne reste donc que (xd²-yc)² ?

CD= racine de (xd²-yc)²
CD=xd²-yc ?

par **zygomatique** » 03 Jan 2015, 12:50

mais lis-tu ce qu'on écrit ? .... :mur:

x_d = x_c !!!!!!!!!!!!

ensuite il serait peut-être bien de calculer y_c en fonction de x_c !!!!!!!!!!!!

par **lywet** » 03 Jan 2015, 13:38

zygomatique a écrit:mais lis-tu ce qu'on écrit ? .... :mur:

x_d = x_c !!!!!!!!!!!!

ensuite il serait peut-être bien de calculer y_c en fonction de x_c !!!!!!!!!!!!

oui j ai compris que xd avait la meme abscisse que xc, mais ils n'ont pas la meme ordonnée, xd² n est pas égal à xc²

Biancoangelo a écrit:
Il faut écrire CD²=(xc-xc)²+(xd²-yc)²
Est ce que cela se simplifie bien en
CD= (xd²-yc) ?

de même, je ne comprends pas comment calculer y_c en fonction de x_c

merci de votre patience,

par **zygomatique** » 03 Jan 2015, 13:50

ne connais-tu pas l'équation de la droite (AB) ?

ne connais-tu pas l'abscisse de C ?

ne peux-tu pas en déduire l'ordonnée de C ?

par **lywet** » 03 Jan 2015, 13:55

equation de la droite:
y=(xa+xb)x-xaxb

Abscisse de C
yc=(xa+xb)x-xaxb

Ordonnée de c:
y=(xa+xb)xc-xaxb
?

par **lywet** » 04 Jan 2015, 18:34

j ai finalement trouvé le polynome:
-xc²+(a+b)xc-ab
Les coordonnées du sommet de la parabole sont (alpha, beta)
j'ai trouvé alpha= (a+b)/2
mais pour beta je trouve : -((a+b)²-4ab)/-4)
Or cela ne correspond pas si l on prend des exemples...
Merci de votre aide

par **zygomatique** » 04 Jan 2015, 19:30

y = (a + b)x - ab

ce qui permet de répondre au problème ...

par **lywet** » 05 Jan 2015, 18:59

zygomatique a écrit:y = (a + b)x - ab

ce qui permet de répondre au problème ...

Merci beaucoup pour toute votre aide,
Lywet

Problème ouvert

Problème ouvert

Qui est en ligne