Problème ouvert

par **isami2005** » 28 Sep 2014, 09:42

[CENTER]Bonjour ! J'ai ce problème à faire et j'ai vraiment du mal...

Soient A et B deux points quelconques de la parabole P d'équation y=x^2.
Soit N un point du segment [AB] et M le point de la parabole P de même abscisse que N. Que peut-dire des valeurs extrêmes de la longueur MN ?

Alors déjà, on sait que lorsque N se déplace, M aussi. Donc lorsque N se rapproche infiniment de A, M se rapproche aussi et inversement avec B. On peut conjecturer que lorsque M et N se confondent avec A ou B MN=0, c'est sa valeur minimale
Et après ça je sais plus quoi faire et comment... Je peux calculer yN et puis yM parce qu'on sait que y=ax + b mais je vois pas où ça va me mener.
Bref, j'espère que quelqu'un pourra me guider un petit peu!
Merci d'avance :lol3: [/CENTER]

par **Sake** » 28 Sep 2014, 09:46

isami2005 a écrit:[CENTER]Bonjour ! J'ai ce problème à faire et j'ai vraiment du mal...

Soient A et B deux points quelconques de la parabole P d'équation y=x^2.
Soit N un point du segment [AB] et M le point de la parabole P de même abscisse que N. Que peut-dire des valeurs extrêmes de la longueur MN ?

Alors déjà, on sait que lorsque N se déplace, M aussi. Donc lorsque N se rapproche infiniment de A, M se rapproche aussi et inversement avec B. On peut conjecturer que lorsque M et N se confondent avec A ou B MN=0, c'est sa valeur minimale
Et après ça je sais plus quoi faire et comment... Je peux calculer yN et puis yM parce qu'on sait que y=ax + b mais je vois pas où ça va me mener.
Bref, j'espère que quelqu'un pourra me guider un petit peu!
Merci d'avance :lol3: [/CENTER]

Salut,

Bonne intuition qualitative de ce qui se passe.
Maintenant, passons au stade supérieur : Tu sais que ce qu'on te pose, c'est un pb d'optimisation. Essaie donc de trouver l'expression de la distance MN en fonction de l'abscisse x. Et après il ne reste qu'à trouver les variations de la longueur MN pour x allant de ??? à ???

par **isami2005** » 28 Sep 2014, 09:54

Sake a écrit:Salut,

Bonne intuition qualitative de ce qui se passe.
Maintenant, passons au stade supérieur : Tu sais que ce qu'on te pose, c'est un pb d'optimisation. Essaie donc de trouver l'expression de la distance MN en fonction de l'abscisse x. Et après il ne reste qu'à trouver les variations de la longueur MN pour x allant de ??? à ???

Merci beaucoup de votre réponse! L'abscisse de M est x et son ordonnée est x^2 puisque le point est sur la parabole ? Donc MN serait égal à lordonnée de N - x^2:
yN - x^2 ?

par **Sake** » 28 Sep 2014, 09:56

isami2005 a écrit:Merci beaucoup de votre réponse! L'abscisse de M est x et son ordonnée est x^2 puisque le point est sur la parabole ? Donc MN serait égal à lordonnée de N - x^2:
yN - x^2 ?

Oui, très bien. Maintenant que vaut

?

Aide : Fais-toi un schéma, c'est TOUJOURS nécessaire.

par **isami2005** » 28 Sep 2014, 09:57

Sake a écrit:Oui, très bien. Maintenant que vaut ?

On pourrait utiliser yN=ax+b mais j'ai voulu essayer tout à l'heure, et sans aucune valeur je ne vois pas où ça nous mène...

par **Sake** » 28 Sep 2014, 09:58

isami2005 a écrit:On pourrait utiliser yN=ax+b mais j'ai voulu essayer tout à l'heure, et sans aucune valeur je ne vois pas où ça nous mène...

Comment fais-tu pour déterminer l'équation d'une droite quand tu sais qu'elle passe par deux points d'abscisses et d'ordonnées connues ?

par **isami2005** » 28 Sep 2014, 09:59

Sake a écrit:Comment fais-tu pour déterminer l'équation d'une droite quand tu sais qu'elle passe par deux points d'abscisses et d'ordonnées connues ?

Avec des vecteurs?

par **Sake** » 28 Sep 2014, 10:04

isami2005 a écrit:Avec des vecteurs?

Oh pourquoi pas. La technique habituelle à ton niveau est de dire que l'équation d'une droite affine du plan est de la forme y : x = ax + b, de trouver a en calculant le taux d'accroissement

et de déterminer b avec une condition donnée, typiquement la connaissance d'un point par où passe la droite.

Mais il y a aussi la possibilité d'aller plus vite en utilisant le produit vectoriel (ou le produit mixte) d'un vecteur directeur de la droite avec le vecteur qui va de A à B.

par **isami2005** » 28 Sep 2014, 10:13

Sake a écrit:Oh pourquoi pas. La technique habituelle à ton niveau est de dire que l'équation d'une droite affine du plan est de la forme y : x = ax + b, de trouver a en calculant le taux d'accroissement et de déterminer b avec une condition donnée, typiquement la connaissance d'un point par où passe la droite.

Mais il y a aussi la possibilité d'aller plus vite en utilisant le produit vectoriel (ou le produit mixte) d'un vecteur directeur de la droite avec le vecteur qui va de A à B.

Ahh :id: !
Je viens d'essayer un peu les deux méthodes, mais encore une fois je ne vois pas comment sans valeur on peut s'en sortir...
Parce que j'ai a= (yB-yA)/(xB-xA) donc y= [(yB-yA)/(xB-xA)]x + b
pour trouver b je peux dire que A est un point de la droite donc ses coordonnées vérifient l'équation donc yA = [(yB-yA)/(xB-xA)]xA + b mais là, bloqué :hum:

Sinon avec les vecteurs, je dis soit W(x;y) un point du plan appartenant à (AB), avec AB son vecteur directeur, je calcule leurs coordonnées et fais le produit en croix pour voir si ils sont colinéaires et tout ça mais encore bloqué :hum:

par **Sake** » 28 Sep 2014, 10:19

isami2005 a écrit:Ahh :id: !
Je viens d'essayer un peu les deux méthodes, mais encore une fois je ne vois pas comment sans valeur on peut s'en sortir...
Parce que j'ai a= (yB-yA)/(xB-xA) donc y= [(yB-yA)/(xB-xA)]x + b
pour trouver b je peux dire que A est un point de la droite donc ses coordonnées vérifient l'équation donc yA = [(yB-yA)/(xB-xA)]xA + b mais là, bloqué :hum:

Sinon avec les vecteurs, je dis soit W(x;y) un point du plan appartenant à (AB), avec AB sont vecteur directeur, je calcule leurs coordonnées et fait le produit en croix pour voir si ils sont colinéaires et tout ça mais encore bloqué :hum:

C'est un problème ouvert, le prof s'attend à ce que tu fasses preuve d'initiatives, quitte à poser tes propres notations, il s'en fiche.

Non tu n'es pas bloqué du tout, tu obtiens facilement que b = yA - [(yB - yA)/(xB - xA)]xA = [xByA - xAyA - xAyB + yAxA]/(xB - xA) = (xByA - xAyB)/(xB - xA)

Sauf qu'une fois ces notations précisées, tu as tout intérêt à considérer que N appartient à la droite d'équation y : x = ax + b pour ne pas inutilement alourdir le travail...

par **isami2005** » 28 Sep 2014, 10:33

Sake a écrit:C'est un problème ouvert, le prof s'attend à ce que tu fasses preuve d'initiatives, quitte à poser tes propres notations, il s'en fiche.

Non tu n'es pas bloqué du tout, tu obtiens facilement que b = yA - [(yB - yA)/(xB - xA)]xA = [xByA - xAyA - xAyB + yAxA]/(xB - xA) = (xByA - xAyB)/(xB - xA)

Sauf qu'une fois ces notations précisées, tu as tout intérêt à considérer que N appartient à la droite d'équation y : x = ax + b pour ne pas inutilement alourdir le travail...

D'accord merci, je vais essayer d'arrêter de me compliquer la vie pour rien :we:
Donc j'obtiens: yN= (xNyB - xNyA + xByA - xAxB) / (xB-xA)
Donc je dois maintenant faire MN = [(xNyB - xNyA + xByA - xAxB) / (xB-xA)] - x^2 ?

par **Sake** » 28 Sep 2014, 10:35

isami2005 a écrit:D'accord merci, je vais essayer d'arrêter de me compliquer la vie pour rien :we:
Donc j'obtiens: yN= (xNyB - xNyA + xByA - xAxB) / (xB-xA)
Donc je dois maintenant faire MN = [(xNyB - xNyA + xByA - xAxB) / (xB-xA)] - x^2 ?

Je préfère toujours que tu remplaces y_N par ax+b, en ayant précisé ce que valent a et b.

par **isami2005** » 28 Sep 2014, 10:38

Sake a écrit:Je préfère toujours que tu remplaces y_N par ax+b, en ayant précisé ce que valent a et b.

Ben c'est ce que j'ai fais là non ? Puisque a= (yB-yA)/(xB-xA) et b= (xByA-xAyB)/(xB-xA)

par **Sake** » 28 Sep 2014, 10:41

isami2005 a écrit:Ben c'est ce que j'ai fais là non ? Puisque a= (yB-yA)/(xB-xA) et b= (xByA-xAyB)/(xB-xA)

Non, écris a et b, ne donne pas leur formule exacte. Juste a, et b. Sinon c'est trop lourd.

par **isami2005** » 28 Sep 2014, 10:47

Sake a écrit:Non, écris a et b, ne donne pas leur formule exacte. Juste a, et b. Sinon c'est trop lourd.

D'accord
Et après ça je fais comment pour trouver les variations de x qui va d'un nombre à un autre ?

par **Sake** » 28 Sep 2014, 10:55

Tu sais calculer des dérivées ?

par **isami2005** » 28 Sep 2014, 11:10

Sake a écrit:Tu sais calculer des dérivées ?

Oui oui
Mais je ne vois pas trop quoi dériver et pourquoi ? :look2:

par **Sake** » 28 Sep 2014, 11:37

isami2005 a écrit:Oui oui
Mais je ne vois pas trop quoi dériver et pourquoi ? :look2:

En fait, la dérivée d'une fonction permet d'en déduire ses variations ! Lorsqu'elle s'annule (à ton niveau), c'est que ta fonction admet un point où elle change de variation, donc qu'elle devient localement minimale ou maximale.

par **paquito** » 28 Sep 2014, 11:38

Soit a l'abscisse de A, b celle de B, N sur [A; B] signifie que

où

décrit

et

que pour la même valeur de

,

;

Donc

et

, comme 2, a et b sont des constantes MN dépend

uniquement de la fonction définie sur

par

ce qui est un jeu d'enfant; le maximum est atteint pour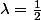

, c'est à

dire quand

est le milieu de

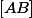et vaut

.

Les calculs sont à vérifier bien sûr; de plus je te donne une caractérisation d'un segment qui n'est pas au programme, mais puisqu'il s'agit d'un problème ouvert, tu as le droit de faire des recherches (c'est ce que tu fais en venant sur ce site), cependant à ta place, je vérifierais par exemple que :

, ce qui justifierais le résultat.

par **chan79** » 28 Sep 2014, 12:28

Salut
Cela fait penser à une propriété des paraboles.
Les milieux de cordes parallèles sont situés sur une parallèle à l'axe des y. Cette parallèle coupe la parabole en un point J et on obtient la tangente en ce point en traçant ici en vert) une parallèle aux autres cordes.
La parabole étant située au dessus de la tangente, on vérifie que la distance MN est maximale si N est le milieu de [AB].
Mais tout ça ne se voit pas au lycée.

Problème ouvert

Problème ouvert

Qui est en ligne