Probleme de matrice

[denver]

Bonjour à tous.

J'ai un problème qui peut parraitre bête mais pourtant je ne vois pas comment le résoudre alors si quelqu'un arrive à m'aider ce serait très sympa.

Je dois écrire une matrice carrée M(3X3) dans Ctels que a^2 est différent de 0 mais a^3 est égal à 0?Est-ce possible avec une matrice 2X2?

En faite, je suis plus intéressé par le raisonnement que la réponse bien sur.

Merci beaucoup

[Cpa]

Salut,

Ce que tu cherches c'est une matrice nilpotente d'ordre 3. On veut lui donner un petit nom, disons A.
N'importe quelle matrice dont le polynôme caractéristique est x^3 sera telle qu'on veut (Cayley-Hamilton)
Je te propose par exemple

En elevant à la puissance la diagonale de 1 va monter...
Et toutes les valeurs propres de A sont nulles : 0 est clairement valeur propre (rang = 2), et si sur la diagonale il y avait autre chose que 0, comme elle est triangulaire, le dét serait 0. Et ce serait mal barré pour être vp.

Maintenant qu'on en a une, tu prends n'importe quelle matrice inversible 3x3 et tu conjugues (si B est une matrice inversible tu fais B*A*B^(-1))

[nuage]

Salut,
tu peux regarder l'application linéaire associée à ta matrice.
Pour que il faut que le noyau soit inclus dans l'image (sinon pour tout n).
Il faut de plus que l'inclusion soit stricte sinon on a .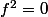
En prenant comme noyau et comme image , on a quelque chose qui fonctionne.
En faisant simple on peut prendre.

Les remarques précédentes permettent également de répondre à la question sur les matrices 2x2

[Cpa]

Oups !
En dim 2, juste un(e?) heuristique :
Une matrice nilpotente c'est une matrice nulle avec une diagonale de 1 mais pas la diagonale pas sur la vraie diagonale (cf la matrice plus haut, parceque c'est pas très clair ^^) donc en dim n tu as n-1 diagonales. Et en elevant à la puissance tu remontes d'une diagonale tes 1. Bon ben, il est impossible d'être nilpotent d'ordre plus que la dimension de l'espace.