Problème de Maths

[nori19]

Les feux de croisement d’une automobile doivent avoir une portée de 30 mètres au moins sans éblouir, pour régler les phares on se place devant un mur et on mesure la hauteur OJ = x où J est le point du mur éclairé par les phares.

HP = 0,6m OH = 3m OJ = x
p(x) = HM

Alors après avoir esssayer , thales , la trigo , soit il me manque une donnée soit j'ai rien compris
pour le moment j'ai fait ça après avoir démontré que (ab) et (hp) sont parallèles :

MH/MO = MP/MJ = OJ/PH

HM = PM[*]OM/MJ = 0,6 *OM/MJ = (30-3)*0,6 /30 = 0,54 m
x= (MH-3)*0,6/MH sauf que je trouve x = 0,54 m est que normalement hm doit faire au moins 30 mètres et ensuite pour trouver OJ il manque pas un donnée ?

[hdci]

Bonjour,

Peux-tu préciser ce que sont tous ces points et toutes ces longueurs et toutes ces droites ?

[nori19]

/Users//Desktop/Capture d’écran 2019-05-04 à 18.30.14.png
4
J'arrive pas à faire une capture d'écran de l'énoncé

[nori19]

[url][https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=2ahUKEwijjZiHsILiAhWw3eAKHRdOBcAQjRx6BAgBEAU&url=http%3A%2F%2Fdaniel.millot1.pagesperso-orange.fr%2Fmaths%2Fbrevet%2Fbrevet_1%2Fprobleme%2Fprobleme_bb1.htm&psig=AOvVaw0zgjPWek670JapXN69c7a_&ust=1557076463976867url]

en remplacent AB par OJ

[nori19]

https://www.google.com/url?sa=i&rct=j&q ... 6463976867

[hdci]

C'est plus clair ! Mais il n'y a pas de point O ni de point J dans l'énoncé...

Alors résulte bien du théorème de Thalès (pourquoi ?) et la dernière partie de la question 1 en découle

Question 2 : il suffit d'utiliser le résultat de la question 1 puisque on a toutes les informations, sauf AM (c'est donc une équation où AM est l'inconnue). Du coup quelle est la valeur de AM ?

[nori19]

Justement c'est ça le problème il manque une donnée prcq je peux pas faire Thales , en vrai il ne manque rien mais du coup comment fait-on pour trouver OJ fin AB sur la figure prcq ça fait 2 inconnue ou il y a un calcul intermédiaire ?

[hdci]

Je ne comprends pas ce que tu écris : à quelle question réponds-tu ?

Reprenons : pour la question 1, as-tu réussi à faire ce qui est demandé ? Attention, dans la question 1, il n'y a aucun calcul et aucune valeur à trouver, il y a juste à établir l'égalité.

[nori19]

Alors pour la question 1 on fait thales et on trouve P(x) = (hm-3)*x/0,6

[nori19]

Mais pour la question 2 on fait comment ?

[hdci]

La question 1 est : démontrer que (AB) est paralèlle à (PH) et que , en déduire que

Ta réponse est

Alors pour la question 1 on fait thales et on trouve P(x) = (hm-3)*x/0,6

Si tu ne respectes pas les notations de l'énoncé ni ne répond correctement aux questions posées, on ne comprend plus rien. Dans la question 1, il n'y a pas de x, il n'y a pas de P(x), et HM est écrit en majuscule et de ssurcroît dans l'autre sens MH.

Du coup je ne comprends pas ta formule. Avec un peu d'effort, je peux trouver que ta division par 0,6, c'est la division par HP, je peux penser que hm c'est MH, mais je ne comprends pas pourquoi HM-3 (cela serait-il égal à MA ?) et je crois comprendre que x c'est ce que tu appelais OJ au tout début et c'est en fait AB, et P(x) c'est HM là aussi comme ce que tu as écrit au tout début de ton post. Tu vois le travail que tu donnes à un correcteur à ne pas respecter les notations de l'énoncé ?

Finalement, si j'ai bien réussi à "deviner" ce que tu as écrit, en le retraduisant avec les appellations de l'énoncé, cela donne



Mais ça c'est faux. Comment arrives-tu à ce résultat ? Est-ce que c'est une étourderie, ou est-ce que c'est parce que tu n'as pas bien compris comment on manipule les divisions et multiplications dans les égalités ?

[nori19]

1. Donner la portée HM en fonction x et on désigne p cette fonction.
2. Déterminer la hauteur OJ afin que la portée soit comprise entre 30 et 45 mètres.

Ce sont les deux questions posées du coup je comprend pas ta réponse

[nori19]

Sachant que OJ est AB car le lien que j'ai donné c'est juste une représentation graphique du problème mais faut pas prendre en compte le reste les deux seules questions sont celles-ci

[hdci]

Ah, mais ce ne sont pas les questions qui sont posées dans le document que tu as mis en lien : voici un copier/coller de ce document tel que je le lis, ajusté en tex :

La distance HM est appelée "la portée du feu de croisement".

Consigne de sécurité:
On admet que cette portée doit, à la fois, être :
d'au moins 30 m, afin d'éclairer suffisamment loin;
d'au plus 45 m, pour ne pas éblouir les autres automobilistes.
PHM est un triangle rectangle en H
Pour l'ensemble du problème, le phare est à une hauteur de PH= 0.60 m et la voiture
est à AH = 3 m du mur.

1) Démontrer que (AB) est parallèle à (PH) et que
En déduire que

Quoi qu'il en soit, la réponse que tu donnes pour la question 1 est fausse. Les triangles sont MHP rectangle en H et MAB rectangle en A, avec M,A,H alignés. Donc (HP) et (AB) sont parallèle car perpendiculaire à la droite (MH) qui est aussi la droite (MA).
On peut donc appliquer le théorème de Thalès car les triangles sont semblables : ce théorème donne une double égalité, que l'on peut synthétiser en "les côtés respectifs des triangles sont proportionnels" ou encore "les nombres (grand côté divisé par petit côté) sont égaux", ou encore "les nombres (petit côté divisé par grand côté) sont égaux".

Quand tu écris P(x)=(hm-3)*x/0,6, en fait tu as écrit ce qui est équivalent à : est-ce que c'est bien dans les deux cas "grand côté divisé par petit côté", ou bien dans le deux cas "petit côté divisé par grand côté" ?

Une fois que tu as corrigé ce détail, l'énoncé pour la question 2 te donne AB=0,58. On sait aussi (début de l'énoncé) que HP=0,6, que AH=3. Comme MA=MH-3 (ce que tu as écrit fort justement), dans la formule on remplace toutes les longueurs par leurs valeurs précédentes (donc AB, HP par des nombres et MA par MH-3) et cela donne une égalité où il y a une seule inconnue qui est MH. C'est donc une équation que l'on sait résoudre et on trouve la valeur exacte de MH.

[nori19]

Enfaite pour la question 1 je dois Donner la portée HM en fonction x et on désigne p cette fonction donc jdois donner une fonction pour HM et j'ai trouvé P(x) = (hm-3)*x/0,6 dont je ne suis pas sur du tout et le texte du lien n'a rien a voir avec mon exercice c'est juste la photo le reste n,'a absolument rien a voir c'est prcq je n'avais pas de photo pour que ça soit plus explicite .

[hdci]

OK donc si je comprends bien : on note la valeur 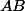et il faut déterminer en fonction de

Cela n'empèche pas que ta formule pour P(x) est fausse car tu as inversé une fraction.

Ensuite, si tu pose HM=P(x) alors tu ne dois plus trouver HM dans ta formule : tu dois remplacer partout HM par P(x).

Bref :

• : corrige cette égalité qui est fausse en conservant HM, AM, x et HP (et en utilisant le théorème de Thalès)
  
• Remplace AM par HM-3 et HP par 0,6, et débrouille-toi pour avoir HM=(une expression dans laquelle il n'y a plus de HM)
  
• Comme HM=P(x) tu as donc obtenu P(x)=(une expression dans laquelle il n'y a que x et des nombres)

[nori19]

Ok , merci mais comment on fait pour se débarasser du HM car on connait pas sa valeur on sait juste qu'il doit être supérieur à 30 mètres mais on peut pas le remplacer par 30 on peut faire P(x) = (HM-3) * x/ 0,6

[hdci]

comment on fait pour se débarasser du HM car on connait pas sa valeur

Pour la première question, on ne connaît pas sa valeur, donc on ne s'en débarrasse pas ! C'est une indéterminée, et HM va dépendre de la valeur x. Pour chaque valeur de x, on va trouver une valeur de HM.
Ceci dit, comme l'énoncé te dis que HM est une fonction de x que l'on note P(x), tu va remplacer HM par P(x) à chaque fois que tu le rencontres.

Toutefois, tu n'as toujours pas traité la correction de ta formule fausse ! Je le redis :
P(x)=(HM-3)*x/0.6 EST FAUX !!!
Car HM=AM*OJ/HP est FAUX !!!

Dans ce que j'ai écrit avant, je t'ai donné toutes les indications pour corriger. Réécrit correctement les égalités du théorème de Thalès en utilisant uniquement HM, AM, OJ et HP et fais-le pas à pas pour que je puisse voir où tu te trompes.

[nori19]

D'abord on démontrer que (OJ) et (HP) sont parallèles ainsi on peut utiliser le théorème de Thales ensuite on écrit l'égalité : MJ/MP = MO/MH = OJ / HP
ainsi HM = OM*HP / OJ = (HM-3)*0,6/x
p(x) = (HM-3)*0,6/x

[hdci]

OK, là c'est correct.
Donc


Maintenant, , donc on peut remplacer par dans la formule ci-dessus : et il n'y a plus de , mais il y a du de chaque côté du signe égal.

Par contre il y a encore un peu de travail, car au final on doit avoir "" suivie par une "formule", une expression algébrique dans laquelle il n'y a que des nombres et la variable .

Indication : comment faire "disparaître" la fraction ici ?