Problème de démonstration
7 messages
- Page 1 sur 1
Problème de démonstration
Bonjour, j'ai un problème avec une démonstration , je dois démontrer que (1/(racine de x +1)-(1/(racine de x -1) est égal à 2/(1-x) pour tout réel x différent de 1. Merci beaucoup pour votre aide! :happy2:
Une égalité à démontrer (méthode en exemple...)
Etudie les variations de la fonction f telle que: ={\frac{1}{\sqrt{x +1}}-{\frac{1}{\sqrt{x -1}}}-{\frac{2}{1-x}}) pour tout
pour tout 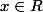 privé de 1.
privé de 1.
iammewtf a écrit:Bonjour, j'ai un problème avec une démonstration , je dois démontrer que (1/(racine de x +1)-(1/(racine de x -1) est égal à 2/(1-x) pour tout réel x différent de 1.
Il faudrait mieux dire pour tout réel >= 1 Merci beaucoup pour votre aide! :happy2:
J'ai répondu un peu vite !
La formule est fausse : l'expression n'est pas valable pour x = 2 !
D'ailleurs comment faire disparaître totalement les radicaux (en mutipliant par la quantité conjuguée) ?
Carpate a écrit:J'ai répondu un peu vite !
La formule est fausse : l'expression n'est pas valable pour x = 2 !
D'ailleurs comment faire disparaître totalement les radicaux (en mutipliant par la quantité conjuguée) ?
Non en effet, j'ai aussi essayé de multiplier par les quantités conjuguées mais la formule qui en ressort n'est pas viable face à d'autres calculs.
Et puis c'est vrai, si on étudie
Jota Be a écrit:Non en effet, j'ai aussi essayé de multiplier par les quantités conjuguées mais la formule qui en ressort n'est pas viable face à d'autres calculs.
Et puis c'est vrai, si on étudie, on finit par s'apercevoir que ça ne vaut pas 0, pour tout x de R\{1}
Et même sans étudier cette fonction ... (définie d'ailleurs sur [1 ; +infini[ et non pour x 0)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
