Probleme avec une démonstration (polynome)

[ennemipublic]

bonjour, j'ai un exercice comme ça dans mon DM, et je ne sais pas du tout par quoi commencer.

"Prouver que si a,b et c désignent 3 entiers tels que "a" different de 0 et |b|=a+c, le polynome ax²+bx+c admet deux racines rationnelles.

La reciproque de cette propriété est-elle vraie?"

Donc voila, je suis completement bloqué, toutes aide est bienvenue pour moi :id:

[Imod]

Remplace dans ton équation b par a+c puis par -a-c et regarde ce qui se passe .

Imod

[ennemipublic]

en remplaçant b par -a-c et a+c on trouve dans les 2 cas
1 et c/a pour (1) et -1 et -c/a pour (2)

Comment démontrer la réciproque? Est-ce possible?

[Imod]

Pour la réciproque , tu supposes que ton équation a deux solutions rationnelles x/y et z/t , elle s'écrit alors a(X-x/y)(X-z/t)=0 , je te laisse finir .

Imod

[ennemipublic]

d'accord, ça ne s'annonce pas facile...
mais est ce que tu peux dire au moins si la réciproque est possible?
P.S ben en fait, j'arrive à rien :mur:

P.S On trouve donc ça :
*cas1:
a(x+c/a)(x+1)
<=>ax²+bx+c

*cas2:
a(x-c/a)(x-1)
<=>ax²+bx+c

donc la réciproque est vraie, mais y a t'il un probleme avec la valeur absolue?

[ennemipublic]

est ce que quelqu'un peut aider? :cry:

[Imod]

Considère par exemple .

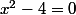
Imod

[ennemipublic]

houla, j'ai rien compri dsl ... :mur:
je m'embrouille encore plus

[Imod]

Cherche les solutions de l'équation et regarde si |b|=a+c , c'est ce que l'on appelle un contre-exemple .

Imod

[ennemipublic]

aaaah j'ai trouvé!!!
bon ben ça marche, en fait j'ai eu une erreur au début, les réponses c'est que -1;-c/a.

[Imod]

J'ai des doutes sur cette dernière intervention mais comme elle est peu détaillée , on peut espérer qu'elle mène quand même à un résultat .

Imod