Probabilité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 21 Mai 2008, 15:32
par sss61 » 21 Mai 2008, 15:32
Voila je suis pas très doué dans les proba, et j'ai un exo que j'ai beaucoup de mal à faire, et j'aurais besoin de conseils poru le continuer et quelques petites pistes svp.
On observe sur une grande période le nombre d'accidents de scooters à un carrefour. Il est alors possible de proposer la modélisation suivante.
Pour n scooters franchissant le carrefour durant une année, on admet que la variable aléatoire Sn qui totalise le nombre d'accidents de scooters à ce carrefour, durant cette année, suit une loi binomiale d'espérance mathématiques E(Sn) = 10.
Soit p la probabilité pour un scooter d'être accidenté à ce carrefour pendant l'année considérée.
1. Calculez p puis donnez l'expression de P(Sn=k) où k est un entier tel que 0 <(ou égal) k <(ou égal) n.
On a E(Sn) = np
donc 10 = np
Donc p = 10/n
P(Sn = k) = (n) p ^k q^n-k
(k)
2. a) Prouvez que ln[P(Sn=0)] = -10*[ln(1-10/n) / (-10/n)] puis déduisez-en lim n->+infini P(Sn=0) =e^-10
b) Démontrez que pour tout entier k, 0 <(ou=) k <(ou=) n-1:
P(Sn=k+1) = P(Sn=k) * (n-k)/(n-10) * 10/(k+1).
c) Démontrez que si lim n->+inf. de P(Sn=k) = e^-10 * [(10^k)/k!] Pour 0 lim n->+inf. de P(Sn=k+1) = e^-10* [(10^k+1)*/(k+1)!] pour 0 < k+1 < n
d) Pouvez en raisonnant par récurrence sur k, que
lim n->+inf. de P(Sn=k) = e^-10 * [(10^k)*k!] (0
3. On suppose que l'entier naturel n est suffisamment grand pour que l'on puisse admettre que e^-10 * 10^k/k! est une approximation acceptable de P(Sn=k). Utilisez cette approximation pour calculer a 10^-4 près, la probabilité qu'au cours de cette année, il y ait au moins 3 accidents de scotters a ce carrefour
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 21 Mai 2008, 16:28
par bombastus » 21 Mai 2008, 16:28
Bonjour,
pour la 2)a,
P(Sn = 0) = (0 parmi n) p ^0 (1-p)^n-0
P(Sn = 0) = (1-p)^n
P(Sn = 0) = (1-10/n)^n
et en calculant ln(P(Sn = 0)), tu devrais arriver au résultat.
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 21 Mai 2008, 18:31
par sss61 » 21 Mai 2008, 18:31
merci ca ma permis d'avancer dans cette question,
j'essaye de démontrer la limite mais pas très facile
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 21 Mai 2008, 19:06
par bombastus » 21 Mai 2008, 19:06
Un indice :
il faut penser à la limite :
lim ln(1+x)/x = 1
x->0
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 12:43
par sss61 » 26 Mai 2008, 12:43
j'ai trouver la limite
je suis passer a la question 2.b)
et je n'arrive pas a trouver a quoi peuvent correspondre ou comment retrouver le (n-k)/(n-10) *10/(k+1)
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 13:23
par bombastus » 26 Mai 2008, 13:23
Il y a plusieurs façon d'y arriver. Je te conseille de partir de P(Sn=k) * (n-k)/(n-10) * 10/(k+1) et d'essayer d'aboutir à P(Sn=k+1) (écrit dans un brouillon l'expression de P(Sn=k+1) pour voir ce à quoi tu veux aboutir).
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 14:09
par sss61 » 26 Mai 2008, 14:09
P(Sn=k+1) = (k+1 parmi n) p^k+1 (1-p)^n-k-1
et pour P(Sn=k) * (n-k)/(n-10) * 10/(k+1) je trouve que c'est égal à:
[(k parmi n) p^k (1-p)^n-k] * 10(n-k)/(nk+n-k-1)
et je suis bloqué ici.
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 14:15
par bombastus » 26 Mai 2008, 14:15
Remplace p par 10/n dans les deux expressions.
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 14:22
par sss61 » 26 Mai 2008, 14:22
P(Sn=k+1) = (k+1 parmi n) (10/n)^k+1 (1-10/n)^n-k-1
et donc P(Sn=k) * (n-k)/(n-10) * 10/(k+1) est égal à:
[(k parmi n) (10/n)^k (1-10/n)^n-k] * 10(n-k)/(nk+n-k-1)
c'est la multiplication entre [(k parmi n) (10/n)^k (1-10/n)^n-k] et 10(n-k)/(nk+n-k-1) que j'arrive pas a faire, je vois pas comment ca peut donner P(Sn=k+1)
je trouve pas la relation :s
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 15:13
par bombastus » 26 Mai 2008, 15:13
Il ne faut y aller calmement, ça va venir tout seul :we:
P(Sn=k+1) = (k+1 parmi n) (10/n)^k+1 (1-10/n)^n-k-1
Donc
P(Sn=k+1) = (k+1 parmi n) (10/n)^k+1 (
(n-10)/n)^n-k-1
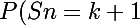 = \frac{n!}{(k+1)!(n-k-1)!}(\frac{10}{n})^{k+1}(\frac{n-10}{n})^{n-k-1}})
celle-là on la laisse de côté pour le moment, c'est le résultat que l'on devra trouver.
P(Sn=k) * (n-k)/(n-10) * 10/(k+1) est égal à:
[(k parmi n) (10/n)^k (1-10/n)^n-k] * 10(n-k)/(nk+n-k-1)
Il ne faut pas développer les parenthèses!
P(Sn=k) * (n-k)/(n-10) * 10/(k+1) = [(k parmi n) (10/n)^k (
(n-10)/n)^n-k] * 10(n-k)/(nk+n-k-1)
Donc (j'ai juste développé k parmi n)
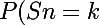 * (n-k)/(n-10) * 10/(k+1) = \frac{n!}{k!(n-k)!}(\frac{10}{n})^k(\frac{n-10}{n})^{n-k}\frac{n-k}{n-10}\frac{10}{k+1}})
Si tu as bien suivi, essaye de voir ce que tu peux modifier pour arriver au résultat voulu.
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 16:36
par sss61 » 26 Mai 2008, 16:36
je te remercie, pour ton aide,
alors je pensait a un arrangement avec le (n-k)/(n-10) qui a linverse peut donner par la suite exposant -1 mais ca me parrait pas très juste :s
après je vois pas trop :s
ca ménerve :briques:
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 16:51
par bombastus » 26 Mai 2008, 16:51
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 17:27
par sss61 » 26 Mai 2008, 17:27
n!/k!(n-k)! = n(n-1)...(n-k+1)*(n-k)/[k! * (k+1)]
(10/n)^k *10 je sais pas
(n-10/n)^n-k 1/(n-10) = (n-10/n)^n-k-1
Les exposant avec les lettres me gènent pas mal et avec les factoriel j'ai du mal
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 17:44
par sss61 » 26 Mai 2008, 17:44
pour le deuxième il me semble avoir une illumination :happy2:
(10/n)^k *10 = 10^k/n^k *10 et
10^k *10 = 10^k+1
enfin il me semble mais j'en suis vraiment pas sur
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 17:52
par bombastus » 26 Mai 2008, 17:52
L'illumination pour le deuxième est bonne :we:
On va continuer avec celle-là :
!}*\frac{n-k}{k+1}})
Ce que tu as écrit :
n!/k!(n-k)! = n(n-1)...(n-k+1)*(n-k)/[k! * (k+1)]
tu développes trop!
!}*\frac{n-k}{k+1}})
=
}*\frac{n-k}{(n-k)!})
Maintenant, k!(k+1)=...
!} = ...})
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 17:59
par sss61 » 26 Mai 2008, 17:59
ha ca va si elle est bonne c'est déja ça :happy:
alors pour
n-k/(n-k)! = 1/(n-k+1)
k!(k+1)= je cherche :hein:
le k! me gène, je ne sais pas comment le transformerou a quoi c'est égal
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 18:05
par bombastus » 26 Mai 2008, 18:05
n-k/(n-k)! = 1/(n-k-1)!
C'est plutôt ça...
k!=k(k-1)(k-2)...*2*1
k!(k+1)=(k+1)k(k-1)(k-2)...*2*1
= ...
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 18:08
par sss61 » 26 Mai 2008, 18:08
k!=k(k-1)(k-2)...*2*1
k!(k+1)=(k+1)k(k-1)(k-2)...*2*1
= (k+1)! ???
-
bombastus
- Membre Complexe
- Messages: 2295
- Enregistré le: 29 Nov 2007, 21:35
-
 par bombastus » 26 Mai 2008, 18:11
par bombastus » 26 Mai 2008, 18:11
Oui!! maintenant que tu l'as vu, tu devras savoir refaire ce type de calcul.
-
sss61
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Avr 2008, 13:29
-
 par sss61 » 26 Mai 2008, 18:12
par sss61 » 26 Mai 2008, 18:12
j'ai regarder en calculant et en remettant tou dans l'ordre et ca me donne presque comme l'autre expression de P(Sn=k+1)
Il me reste plus ça a savoir si c'est bon:
(n-10/n)^n-k * 1/(n-10) = (n-10/n)^n-k-1
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
