Probabilité

[tommylebro]

Bonjour voilà maintenant un bout de temps que je reste figé sur ce problème, auriez vous des conseils pour me permettre d'avancer merci, voici le problème :
Gabin est un spécialiste des lancers francs au basket
Chacun de ses lancers est indépendant du précédent
Gabin affirme qu'il a au moins 60% de chance de réussir exactement un lancer sur deux.
A-t-il raison ?
Conseil : appeler x la proba de réussir un lancer franc pour une tentative et construire un arbre de probabilités.

[ortollj]

deja je trouve qu'il a la peche, a 115 ans jouer encore au basket ?, chapeau mon Jean !
snon ca va au niveau du troll toi ?

[ortollj]

sinon ca y est moi j'ai deja construit mon arbre

[beagle]

Troll?
C'est vrai que cela surprend cet énoncé.

alors voici comment avancer?

Les lumières du gymnases sont capricieuses.
Lorsque Gabin fait son lancer on est soit en lumière allumée, soit en lumière éteinte et ce de façon indépendante, c'est à dire que savoir si c'était allumé ou éteint juste avant ou sur une durée x avant ne renseigne en rien sur la proba que cela soit allumé ou éteint au k ièm lancer.

Donc lumière allumée, Gabin réussit 50% des lancer , exactement , pour sur , c'est du sur.
lumière éteinte il réussit 0% des lancers.

On sait que la lumière reste allumée au moins 60% du temps.

Donc dans au moins 60% des cas il a 50% de réussite au lancers.

Ensuite on peut affecter un % de réussite également lumière éteinte.
je pense que les gars à 50% de réussite le font aussi les yeux fermés avec un % non négligeable.
Alors il faut faire des probas conditionnelles, car cela permet d'avoir la lumière allumé dans plus que les 60% du temps pour avoir finalement du 50%.

ensuite on peut exprimer le % lumiere allumée, le % lumiere éteinte et le % de temps lumière allumée...pour satisfaire les conditions

Quant à la probabilité de tomber sur un exo comme cela au lycée , je dirais faible,
enfin j'espère!

[GaBuZoMeu]

Je ne comprends pas pour quoi la question attire ce genre de réponse. Je trouve que c'est une question amusante, et assez astucieuse.
Il n'y a qu'à suivre l'indication : si est la probabilité de réussir un lancer, quelle est la probabilité de réussir exactement un lancer sur deux lancers indépendants ? Cette probabilité peut-elle être égale à 0.6 ?

[beagle]

Ben pourquoi ce que j'ai dit serait hors de propos.
Les conditions que j'ai mises réalisent des lancers indépendants, sachant les lancers précédents ne permet pas de dire si lumiere allumée ou éteinte au suivant, et alors 1 sur deux de façon indépendante également si allumé.
si la lumiere est allumée dans au moins 60% des cas, ben dans au moins 60% des cas j'ai une chance sur deux
avec des lancers indépendants, non?

[beagle]

Une autre, Gabin lance le ballon de façon aléatoire et indépendante
dans 60% des cas avec la main droite, il réussit alors 50% des tirs
dans 40% des cas avec la main gauche, il réussit 0% des tirs

Gabin a alors raison.
Et le prof astucieux?

[GaBuZoMeu]

C'est quoi ce délire, beagle ?

Une version géométrique du problème : la somme des aires des rectangles peut-elle faire 60% de l'aire du grand carré ?

[beagle]

c'est pas du délire,
les profs se battent gentiment pour savoir si un chemin a une probabilité QS discussions précédentes.
La proba c'est pour un évènement, pas pour un chemin crient-ils effarouchés.
Bon c'est idiot puisque le chemin EST la proba que l'évènement POSSEDE.

Alors ici cela ne dérange personne que 60% ne soit pas un évènement, tout comme le 50%.
L'intitulé tel qu'il est écrit signifie qu'il ya un évènement A qui se réalise dans 60% des cas et qui alors a 50% d'etre gain ou perte.
Donc j'ai donné deux exemples, le dernier est moins idiot que le premier où on peut avoir dans 60% des cas avec la main droite gain dans 50%

[beagle]

pièce pile ou face bien équilibrée
Beagle affirme qu'il a au moins 100 % de chance de réussir exactement un lancer sur deux en moyenne retombant sur pile.
Beagle a-t-il raison?

(et au plus aussi pour ètre honnète)

[GaBuZoMeu]

On voit que c'est le week-end !

[beagle]

On voit que c'est le week-end !

je veux bien voir la solution avec un arbre de proba

et la même en théorie ensembliste puisque j'aime bcp le carré de 1 divisé en deux par la p(A) et dans l'autre sens divisé en deux par la p(B) c qui nous fait les 4 ensembles comme sur ta figure géométrique.

donc que doit-on voir en semaine?

[GaBuZoMeu]

C'est l'exercice de tommylebro.
Je suggère qu'on le laisse y réfléchir. Je ne suis pas sûr que tu l'aies beaucoup aidé, et peut-être vaudrait-il mieux que tu t'abstiennes de faire le malin.

[beagle]

C'est l'exercice de tommylebro.
Je suggère qu'on le laisse y réfléchir. Je ne suis pas sûr que tu l'aies beaucoup aidé, et peut-être vaudrait-il mieux que tu t'abstiennes de faire le malin.

ça c'est terriblement une nouvelle fois prétentieux.
Ortollj a le premier pensé à un troll, or Ortollj a un niveau de maths qui dépasse le lycée.
Lycéen95 a répondu dans le fil et cela ne semblait pas lui parler, je crois qu'il est prof de maths.
Et perso je ne fais pas le malin sur cet exo, j'ai essayé de comprendre les phrases du problème, sur les probas de niveau lycée je ne me trouve pas déplacé pour répondre en général, et là honnêtement de quoi parle-t-on, euh?
Donc dire que je fais le malin n'est pas très correct.

Je dirai une chose néanmoins.L'arbre de probabilité est à enseigner pour servir de support au raisonnement dans les problèmes de probas. Donc j'attends de voir comment l'arbre de proba va aider à déméler ce truc.
Et c'est idem avec le support ensembliste que j'adore, sauf que dans ton problème géométrique on ne voit pas le 0,5 ni le 0,6...
Je vais attendre mais bon
Sur ce qui semble ètre la réponse (avec tes indications qui laissent supposer que…) je ne trouve pas cela malin,
làoù tu vois de l'astuce. Mais il ya peut-tre une représentation qui va m'éclairer

[tommylebro]

Salut à tous et merci des réponses, dans un premier temps je tiens à signaler que ce n'est pas un troll comme certain ont pu le dire ou alors ma prof de math m'en veux, je vais essayer de relire vos indications et de me débrouiller je mettrais ici la solution que la prof nous donnera, si vous avez d'autres conseils n'hésitez pas.

[GaBuZoMeu]

@ beagle : C'est le problème récurrent avec les exercices "habillés". Il y a en général de l'implicite. Je trouve que dans le genre, on fait pire que cet exercice.
Ça serait moins "sexy" si l'énoncé de l'exercice était :
Soient et deux variables aléatoires de Bernoulli indépendantes de même paramètre . Existe-t-il un tel que la probabilité de 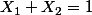soit égale à 60% ?
Mais c'est exactement le contenu de l'exercice (ça me semble clair, et si ni lycéen95 ni ortolij ne le voient, qu'y puis-je ?)

@tommylebro : j'espère bien que tu n'auras pas besoin d'attendre que ta prof te donne la solution. Reviens vers nous pour nous expliquer ce que tu tentes. Le fait que tu aies posté la même question sur plusieurs forums fait mauvais effet, ça explique peut-être une partie des réactions négatives.

[tommylebro]

@GaBuZoMeu Merci encore, oui en effet suite à une erreur de ma part j'ai posté dans un premier temps la question dans la partie "Collège" donc je comprend mais je ne m'y attendais pas tout de même, pas de soucis je vous tient au courant, d'un côté est il possible de trouver la réponse ? Histoire de savoir si problème est totalement solvable car dans toutes ces réponses je suis un peu perdu

[GaBuZoMeu]

Oui, le problème est parfaitement résoluble.
Reprenons.
À chaque lancer, Gabin a la probabilité x de réussir.
Gabin affirme qu'il a 60% de chance de réussir exactement une fois en lançant deux fois (les réussites aux deux lancers sont indépendantes). Est-ce possible ?
Bien entendu, tu dois commencer par calculer en fonction de x la probabilité pour qu'il y ait exactement une réussite (pas zéro, pas deux) sur les deux lancers.

[tommylebro]

Merci beaucoup je vais essayé

[ortollj]

désolé d'avoir pris l'ennoncé de cet exercice pour un troll, effectivement on ne peut atteindre les 60%.
je vous presente mes excuses.oui je trouve que dessiner l'arbre aide a résoudre le probleme.
@tommylebro dessine l'arbre a 4 branches avec les proba x et 1-x