DM T°S probabilité

[bichik77]

Bonjour, je bloque sur le dernier exercice de mon DM et sur une question en particulier. (désolé d'avance mais je ne sais pas faire les indices donc c'est possible qu'il est des incompréhensions)

Soit une fourmi sur un tétraèdre ABCD qui se déplace aléatoirement sur ses arêtes d'un sommet à un autre, avec une équiprobabilité dans le choix du sommet à atteindre. La fourmi par du sommet A.
On note a"indice"n, b"indice"n, c"indice"n et d"indice"n les probabilités que la fourmi soit respectivement en A,B,C et D après n déplacement.
On à donc: a0=1 et b0=c0=d0=0

1) déterminer an, bn, cn et dn pour n=1 et n=2.
==> a1=0 et b1=c1=d1=1/3 ; a2=1/3 et b2=c2=d2=2/9 (résultat trouvés via la formule des probabilité total)

2) démontrer: a"indice"n+1 = (1/3)(1-a"indice"n)
==> c'est là que je bloque. je ne suis pas sur d'avoir le bon raisonnement :/
On peut déjà établir l'égalité: 1-an= bn+cn+dn. Après , étant donné que la fourmi part du sommet A, a"indice"n+1 signifie qu'elle s'est déplacée sur un autre sommet que A donc a"indice"n+1=0 et b"indice"n+1=c"indice"n+1=d"indice"n+1=1/3.
Ici je ne c'est pas comment raisonner pour arriver à la conclusion qu'il faut faire la somme des probabilité b"indice"n+1, c"indice"n+1 et d"indice"n+1 ( car si on fait la somme on obtient le résultat voulu).

Voilà j'ai exposé le problème, j'espère que vous comprendrez et que vous pourrez m'aider. Merci d'avance.

[Ben314]

Salut,
Tu fait... la même chose qu'au 1) mais de façon un peu plus théorique, c'est à dire la formule des proba totales.
ça va te donner (<- a_{n+1} entouré d'une balise "TEX") en fonction de , et 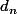et tu utilisera l'égalité que tu as déjà observée (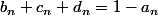) pour conclure.

[titine]

Moi j'utiliserai un arbre indiquant la position de la fourmi après n dé placements et après (n+1) déplacements.

Après n déplacement elle est soit en A (avec une probabilité an) , soit en B (avec une probabilité bn) , soit en C , soit en D.
Tu as donc 4 branches.

Si , après n déplacements elle est arrivée en A, après le déplacement suivant elle sera soit en B, soit n C, soit en D, la probabilité de chacune de ces possibilités est 1/3. Donc à partir de A 3 branches.
De même si elle est arrivée en B ou en C ou en D.

Maintenant, a(n+1) = probabilité d'avoir A après n+1 déplacements
= P(An inter An+1) + P(Bn inter An+1) + P(Cn inter An) + P(Dn inter An)
= 0 + bn*1/3 + cn*1/3 + dn*1/3
Je ne sais pas si je suis très clair ...

Donc a(n+1) = 1/3 (bn + cn + dn)
Et comme tu l'as remarqué : an + bn + cn + dn = 1
Donc bn + cn + dn = 1 - an

[Ben314]

@titine : en fait, "faire un arbre" ou "utiliser la formule des proba totales ", c'est exactement la même chose : l'arbre étant la représentation "graphique" de la formule des proba. totales.
J'ai utilisé cette expression plutôt que "arbre" du fait que bichik77 l'avait employé pour expliquer comment il avait trouvé les résultats du 1)

[titine]

@titine : en fait, "faire un arbre" ou "utiliser la formule des proba. totales", c'est exactement la même chose : l'arbre étant la représentation "graphique" de la formule des proba. totales.
J'ai utilisé cette expression plutôt que "arbre" du fait que bichik77 l'avait employé pour expliquer comment il avait trouvé les résultats du 1)

Oui, oui, tout à fait d'accord

[bichik77]

Merci à vous pour votre aide :) j'aurai pas pensé à utiliser la formule des probabilités totales pour cette question. Et merci Ben314 pour la balise TEX, les égalités sont tout de suite plus propres et plus lisibles :lol3: