Bonjour, j'ai une ptite question:
J'ai un évènement A qui a une probabilité de se réaliser de 20% disons ( 80% de rater), et cette évènement me coûte 10 euros à chaque fois.
Je voudrais savoir combien de fois il faudra que je tente d'essais pour réaliser A/combien ça va me coûter.
Merci. :help:
Probabilité
3 messages
- Page 1 sur 1
Tu ne pourras pas calculer une somme ou un nombre de coups avec certitude mais seulement l'espérance (la moyenne) de la somme qu'il te faudra probablement dépenser.
Pour cela tu imagines un arbre infini :
soit au premier coup ça marche (prob p) et tu as dépensé 10 et le jeu s'arrête
soit ça a raté et tu dois recommencer et de nouveau
ça marche (p) et tu as dépensé 20 soit ça rate
Ton espérance de dépense sera donc
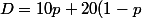p + 30(1-p)^2p+ ... +10n(1-p)^{n-1} p)
Pour trouver cette somme et faire tendre n vers l'infini, mets d'abord 10p en facteur puis appuis toi sur la formule
1+q+...+q^n+ .... = 1/(1-q) et dérives là des deux cotés
je te laisse finaliser tout ça pour voir si tu as tout bien compris ?
[EDIT : grillé, j'ai été trop lent ;+) ]
Pour cela tu imagines un arbre infini :
soit au premier coup ça marche (prob p) et tu as dépensé 10 et le jeu s'arrête
soit ça a raté et tu dois recommencer et de nouveau
ça marche (p) et tu as dépensé 20 soit ça rate
Ton espérance de dépense sera donc
Pour trouver cette somme et faire tendre n vers l'infini, mets d'abord 10p en facteur puis appuis toi sur la formule
1+q+...+q^n+ .... = 1/(1-q) et dérives là des deux cotés
je te laisse finaliser tout ça pour voir si tu as tout bien compris ?
[EDIT : grillé, j'ai été trop lent ;+) ]
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
