Bonjour. IL y a un exercice de mon DM dans lequel j'ai du mal .
L'énoncé est : Soit un entier n non nul. On lance n fois de suites deux dés cubiques bien équilibrés
On note:
An, l'événement "on a obtenue au moins un double six au cours de ces n lancés"
Bn l'événement contraire de An ( je sais pas comment on fait " A avec une barre au dessus " )
Pn=p(An)
1)a) ON suppose ici que n=1 Montrer que p1=1/36
Il y a 36 issue et 1 chance d'avoir un double 6 => 1/36
1)b)On suppose que ici n=2 . Calculer p(B2). En déduire p2
A savoir que on fait 2 lancés , a chacun de ces lancés la probabilité de faire un double 6 est de 1/36 donc la probabilité d'avoir un double 6 est 1/36 , p(B2) est donc 35/36
Voilà ce que j'ai "réussi" a faire c'est la partie proba
2) Montrer que pour tout entier n>ou égale 1 , p(Bn) = (35/36)n. En déduire l'expression de Pn en fonction de n
3) étudier les variations de p et interpréter le résultat je devrais réussir je pense ce n'est pas très compliqué suffit de faire dérivé , tableau de signe puis tableau de variation
4) A l'aide de la calculatrice, déterminer le nombre minimale de lancer pour que la probabilité d'obtenire au moin un double six lors de ces lancers soit supérieur a :
a) 0,5 b) 0,9 c) 0,99
Quelle est la limitte de la suite p ? Interpréter le résultat ?
J'ai marqué tout l'énoncé mais la question ou j'ai du mal n'est que la 2 ( la 4 aussi ) .
pour la 2 j'ai trouvé (1/36) n
DM proba/suite
10 messages
- Page 1 sur 1
L'évènement contraire "A barre" est donc "on n'obtient aucun double 6 sur les n lancés".
Si on regarde tous les couples possibles :
(1, 1)
(1, 2)
...
(6, 6)
On voit qu'il y en a 36 et qu'un seul est (6, 6), on a donc le nombre de cas de l'évènement divisé par le nombre de cas total pour 1 lancé (n = 1)
Soit = 35/36)
Cela signifie qu'en lançant une fois on a 35/36 chance de ne pas faire un double 6.
Sur n lancé, la proba est donc de n fois 35/36.
Si est la proba inverse c'est-à-dire la proba de faire un double 6 sur n lancé. Alors avec le même raisonnement c'est le nombre de couples correspondant à l'évènement (cette fois seulement (6,6) donc 1) sur le nombre de couple. 1/36.
est la proba inverse c'est-à-dire la proba de faire un double 6 sur n lancé. Alors avec le même raisonnement c'est le nombre de couples correspondant à l'évènement (cette fois seulement (6,6) donc 1) sur le nombre de couple. 1/36.
correction : pour n = 1 ok, reste à trouver pour n.
Si on regarde tous les couples possibles :
(1, 1)
(1, 2)
...
(6, 6)
On voit qu'il y en a 36 et qu'un seul est (6, 6), on a donc le nombre de cas de l'évènement divisé par le nombre de cas total pour 1 lancé (n = 1)
Soit
Cela signifie qu'en lançant une fois on a 35/36 chance de ne pas faire un double 6.
Sur n lancé, la proba est donc de n fois 35/36.
Si
correction : pour n = 1 ok, reste à trouver pour n.
kelthuzad a écrit:L'évènement contraire "A barre" est donc "on n'obtient aucun double 6 sur les n lancés".
Si on regarde tous les couples possibles :
(1, 1)
(1, 2)
...
(6, 6)
On voit qu'il y en a 36 et qu'un seul est (6, 6), on a donc le nombre de cas de l'évènement divisé par le nombre de cas total pour 1 lancé (n = 1)
Soit
Cela signifie qu'en lançant une fois on a 35/36 chance de ne pas faire un double 6.
Sur n lancé, la proba est donc de n fois 35/36.
kelthuzad : Ta remarque est bonne, mais ne faudrait-il pas remplacer "fois" par une puissance ?
Non car on veut faire au moins une fois quelque chose, on est donc sur une somme. On généralise par n lancés donc une multiplication par n.
Une puissance serait là si l'évènement était de vouloir obtenir un même résultat à chaque essai.
Obtenir 3 fois de suite (6,6) c'est une proba, dans cet autre cas plus n est grand plus la proba diminue, on s'en rend bien compte.
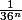
Une puissance serait là si l'évènement était de vouloir obtenir un même résultat à chaque essai.
Obtenir 3 fois de suite (6,6) c'est une proba, dans cet autre cas plus n est grand plus la proba diminue, on s'en rend bien compte.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
