bonjour a tous!
voici un exercice que j'ai fait mais je pense que je me suis trompé dans mes résultats pouvez-m'aider pr les corrigés ? :hein:
voici l'énoncé:
I=intégral de0à1 dx/racine(x²+2); J=intégral de 0à1 (x²)/ racine(x²+2)dx et K=intégral de 0à1 racine(x²+2)
1)Soit la fonction f définie sur [0;1] par f(x)= ln(x+(x²+2)
a)Calculer la dérivée de f(x)= racine(x²+2)
Je trouve (2x)/(2racine(x²+2)
b) En déduire la dérivée f' de f
Je trouve ln(2racine(x²+2)+2x)/(2x²+x+4)
c)Calculer I
2)je trouve 8racine17 :doh:
a) Sans calcule explicitement J et K,vérifier que: J+2I=K :hein:
Ici je pensais calculé en remplaçant j et i par leur fonction mais c'est dit ds la consigne sans calcule donc je vois pas trop quoi faire!
b)Al'aide d'une intégration par parties portant sur K, montrer que:
K=racine(3)-J
c) En déduire que J et K.
merci de m'aider pour cette exercice :we:
Primitive
11 messages
- Page 1 sur 1
Bon allez on reprend tout et on corrige ton énoncé...
Alors en fait, on cherche
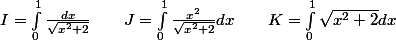
On pose
telle que = ln(x + \sqrt{x^2+2}))
1)a) = \sqrt{x^2+2})
On a = \frac {2x}{2\sqrt{x^2+2}} = \frac {x}{\sqrt{x^2+2}})
D'où la dérivée de f :
 = \frac {1+g'(x)}{x+g(x)} = \frac {1+\frac {x}{\sqrt{x^2+2}}}{x + \sqrt{x^2+2}} = \frac {\frac {\sqrt{x^2+2} + x}{\sqrt{x^2+2}}}{x + \sqrt{x^2+2}} = \frac {1}{\sqrt{x^2+2}})
c) Calculer I
Donc on vient de trouver une dérivée de la fonction f, et on s'aperçoit que I est l'intégrale de 0 à 1 de f '
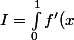dx = \left [ f(x) \right ]_0^1 = f(1) - f(0) = ln(1+\sqrt{3}) - ln(\sqrt{2}))
Voilà déjà ça, essai de comprendre et surtout pose des questions au lieu de tout balancer comme ça
Alors en fait, on cherche
On pose
telle que
1)a)
On a
D'où la dérivée de f :
c) Calculer I
Donc on vient de trouver une dérivée de la fonction f, et on s'aperçoit que I est l'intégrale de 0 à 1 de f '
Voilà déjà ça, essai de comprendre et surtout pose des questions au lieu de tout balancer comme ça
primitves
oooh désolé dans l'énoncé je me suis trompé mais noker a eu bon; enfaite dans la dérivée je pensais que ln u(x)= ln (u'(x)/u(x)) alors que c'est
ln u(x)=u'(x)/u(x) et en plsu j'oublie toujours de simplifier.
Par contre comme j'ai du mal pour les primitives je comprend pas comment tu as trouvé la primitive de (dx)/(racine(x²+2))??????? :hein:
ln u(x)=u'(x)/u(x) et en plsu j'oublie toujours de simplifier.
Par contre comme j'ai du mal pour les primitives je comprend pas comment tu as trouvé la primitive de (dx)/(racine(x²+2))??????? :hein:
salut,
je n'ai pas suivi les calculs mais on te donne tout dans l'ennoncé
on te dit de verifier que J+2I=K ds le (a) et que K=racine(3)-J ds le (b) donc tu obtiens un systeme qui va te permettre de trouver la valeur de J et K
 tu connais I donc...
tu connais I donc...
je n'ai pas suivi les calculs mais on te donne tout dans l'ennoncé
a) Sans calcule explicitement J et K,vérifier que: J+2I=K
Ici je pensais calculé en remplaçant j et i par leur fonction mais c'est dit ds la consigne sans calcule donc je vois pas trop quoi faire!
b)Al'aide d'une intégration par parties portant sur K, montrer que:
K=racine(3)-J
c) En déduire que J et K.
on te dit de verifier que J+2I=K ds le (a) et que K=racine(3)-J ds le (b) donc tu obtiens un systeme qui va te permettre de trouver la valeur de J et K
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
