Bonjour,
Non il n'y a pas de formule directe pour la primitive de 1/u.
ln(u) c'est une primitive de u'/u.
Primitive de 1/u
11 messages
- Page 1 sur 1
Re: Primitive de 1/u
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
Bonjour,
il faut transformer ton dénominateur de façon à faire apparaître une expression de la forme
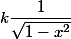 avec k = constante ; tu peux facilement trouver une primitive de la fraction
avec k = constante ; tu peux facilement trouver une primitive de la fraction
il faut transformer ton dénominateur de façon à faire apparaître une expression de la forme
Re: Primitive de 1/u
Le truc c'est que je doute qu'au lycée (en France du moins mais peut-être que lazare n'est pas lycéen en France ?) on connaisse la dérivée de l'arcsinus...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
Il y a quelques (dizaines d')années, c'était effectivement du niveau de la terminale C ; je ne sais plus si c'était au programme, mais je me souviens qu'en 82 mon prof de math m'avait demandé en exercice "au tableau à la volée" de calculer la dérivée de l'arccosinus).
Toujours est-il qu'avec une mise en forme canonique du polynôme on arrive à faire apparaître du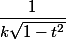 et cela s'intègre ensuite aisément.
et cela s'intègre ensuite aisément.
Toujours est-il qu'avec une mise en forme canonique du polynôme on arrive à faire apparaître du
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
On a
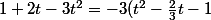=-3\Big((t-\frac{1}{3})^2-\frac{10}{9}\Big))
(On retrouve cela en considérant que t²-2t/3 est le début d'une identité remarquable, et on complète)
Pour avoir la forme 1-t², on va mettre -10/9 en facteur et cela donne
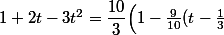^2\Big)=\dfrac{10}{3}\Bigg(1-\Big({\frac{3}{\sqrt{10}}(t-\frac{1}{3})\Big)^2\Bigg))
En posant alors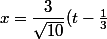) on a maintenant
on a maintenant
)
Ce qui fait que
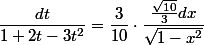
Soit après simplification (et en espérant que je n'aie pas fait d'erreur de calcul)
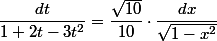
Donc, sauf erreur
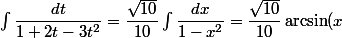)
(On retrouve cela en considérant que t²-2t/3 est le début d'une identité remarquable, et on complète)
Pour avoir la forme 1-t², on va mettre -10/9 en facteur et cela donne
En posant alors
Ce qui fait que
Soit après simplification (et en espérant que je n'aie pas fait d'erreur de calcul)
Donc, sauf erreur
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
Ah oui je me disais cette racine de 10 était bizarre...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
Ce n'est pas "le même" k. Tu peux remplacer k par C par exemple dans la première pour avoir
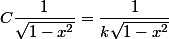
puisque k ou C est une constante elle ne change pas le mécanisme puisqu'on peut la conserver en facteur dans la recherche de la primitive.
Par ailleurs, j'ai un peu complexifié dans la démarche (avec les dx, dt etc.), ça faisait longtemps que je n'avais pas fait ce genre d'exo. En fait, il suffit de se souvenir que si F(t) est une primitive de f(t), alors}{a}) est une primitive de
est une primitive de )
Comme une primitive de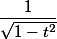 est
est )
on a donc directement le fait qu'une primitive de^2}}) est
est }{a})
Donc une primitive de^2}}) est
est }{a})
Et une primitive de^2}}) est
est }{ka})
D'où le fait de transformer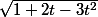 en
en ^2})
puisque k ou C est une constante elle ne change pas le mécanisme puisqu'on peut la conserver en facteur dans la recherche de la primitive.
Par ailleurs, j'ai un peu complexifié dans la démarche (avec les dx, dt etc.), ça faisait longtemps que je n'avais pas fait ce genre d'exo. En fait, il suffit de se souvenir que si F(t) est une primitive de f(t), alors
Comme une primitive de
on a donc directement le fait qu'une primitive de
Donc une primitive de
Et une primitive de
D'où le fait de transformer
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
Comme l'a indiqué Pisigma
J'ai fait une erreur en factorisant par -3 il devrait y avoir -1/3 et non -1 dans la parenthèse. donc au final on trouve
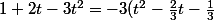=-3\Big((t-\frac{1}{3})^2-\frac{4}{9}\Big))
Je ne comprends pas la question : est-ce "pourquoi n'ai-je pas factorisé" ? Si c'est cela la question, la raison est que l'on veut avoir 1-x² dans la racine et pas (x-a)(x-b) qui ne donnerait rien. Or la forme canonique d'un polynôme du second degré est^2+\beta) et justement cette forme canonique peut aboutir à la forme 1-x² après avoir factorisé par bêta (s'il est strictement négatif) et poser x=....
et justement cette forme canonique peut aboutir à la forme 1-x² après avoir factorisé par bêta (s'il est strictement négatif) et poser x=....
La technique est donc ici d'utiliser la forme canonique pour faire apparaître ce 1-x²
Pisigma a écrit:Bonsoir hdci,
je pense qu'il y a une petite coquille au début
J'ai fait une erreur en factorisant par -3 il devrait y avoir -1/3 et non -1 dans la parenthèse. donc au final on trouve
lazare a écrit:Pourquoi ici tu utilise le polynôme sans la racine ?
Je ne comprends pas la question : est-ce "pourquoi n'ai-je pas factorisé" ? Si c'est cela la question, la raison est que l'on veut avoir 1-x² dans la racine et pas (x-a)(x-b) qui ne donnerait rien. Or la forme canonique d'un polynôme du second degré est
La technique est donc ici d'utiliser la forme canonique pour faire apparaître ce 1-x²
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Primitive de 1/u
En re-détaillant les calculs :
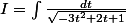
On met le radicande R (trinôme du second degré) sous forme canonique :
= -3[(t-\frac13)^2-\frac19-\frac13]=-3[(t-\frac13)^2-\frac49])
^2=\frac43[1-\frac94(t-\frac13)^2]=\frac43[1-(\frac{3t-1}{2})^2])
Changement de variable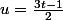
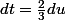
+C)
On met le radicande R (trinôme du second degré) sous forme canonique :
Changement de variable
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
