Primitive
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
GFX
- Membre Naturel
- Messages: 18
- Enregistré le: 27 Oct 2011, 17:44
-
 par GFX » 19 Nov 2011, 17:55
par GFX » 19 Nov 2011, 17:55
Bonsoir,
Je n'arrive pas a faire la primitive de

J'essaye de faire quelque chose comme ce-ci
^{-1/2} = \dfrac{3x^2.sqrt{(x-1)^3}}{3/2} - \int \dfrac{6x.sqrt{(x-1)^3}}{3/2})
Mais c'est surement pas comme ça que l'on doit faire.
Merci pour votre aide.
-
low geek
- Membre Relatif
- Messages: 318
- Enregistré le: 02 Jan 2011, 19:09
-
 par low geek » 19 Nov 2011, 18:10
par low geek » 19 Nov 2011, 18:10
Bonsoir,
C'est un peu compliqué ça.
Je pense qu'il faut remarqué que

Or

Ce sera plus facile pour l'intégration par partie (il faudra en faire 3 pour simplifier petit a petti les puissances)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 19 Nov 2011, 18:21
par fibonacci » 19 Nov 2011, 18:21
Bonsoir;
on pose


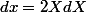
la primitive devient
^3}{X}\times2XdX)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 19 Nov 2011, 18:29
par fibonacci » 19 Nov 2011, 18:29
Puis
en simplifiant et en développant
dX)
on intégre le polynôme et on remplace

par
)
-
GFX
- Membre Naturel
- Messages: 18
- Enregistré le: 27 Oct 2011, 17:44
-
 par GFX » 19 Nov 2011, 19:11
par GFX » 19 Nov 2011, 19:11
fibonacci a écrit:Bonsoir;
on pose


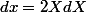
la primitive devient
^3}{X}\times2XdX)
Merci mais
Je comprend jusque

Aprés je ne comprend plus
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 20 Nov 2011, 04:43
par fibonacci » 20 Nov 2011, 04:43
Bonjour;
1) on fait un changement de variable
je pose

puis on défini

par rapport


puis il faut déterminer la différentielle dx par rapport à X pour cela on peut prendre
2 possibilités
prendre
^,=(X^2)^,)
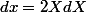
ou
^,=(X)^,)

Récapitulons on a:


^3)
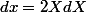
d'où
^3^}{X}2XdX=2\int(X^2+1)^3dX})
on développe le polynôme en se servant de l'identité remarquable
^3=a^3+3a^2b+3ab^2+b^3)
puis on intègre terme à terme.
^{{{7}\over{2}}}}\over{7}}+....+...+2\sqrt{x-1})
-
GFX
- Membre Naturel
- Messages: 18
- Enregistré le: 27 Oct 2011, 17:44
-
 par GFX » 21 Nov 2011, 17:00
par GFX » 21 Nov 2011, 17:00
Merci beaucoup, je comprend mieux
ce qui donne donc
^3}{7}+\dfrac{3(x-1)^2}{3}+\dfrac{3(x-1)}{3}+1))
-
Black Jack
 par Black Jack » 21 Nov 2011, 17:23
par Black Jack » 21 Nov 2011, 17:23
GFX a écrit:Merci beaucoup, je comprend mieux
Attention que le changement de variable n'est pas, je pense, au programme en Secondaire.
:zen:
-
GFX
- Membre Naturel
- Messages: 18
- Enregistré le: 27 Oct 2011, 17:44
-
 par GFX » 21 Nov 2011, 17:26
par GFX » 21 Nov 2011, 17:26
Black Jack a écrit:Attention que le changement de variable n'est pas, je pense, au programme en Secondaire.
:zen:
Si mais je n'etais pas la quand le prof a expliqué
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 26 Nov 2011, 05:06
par fibonacci » 26 Nov 2011, 05:06
Bonjour;
^3=2\,X^6+6\,X^4+6\,X^2+2)
dX}={{2\,X^7}\over{7}}+{{6\,X^5}\over{5}}+2\,X^3+2\,X)
en remplaçant

par
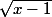
^{1/2}\to{{2\,X^7}\over{7}}=((x-1)^{1/2})^7=(x-1)^{\frac{7}{2})
d'où
^{{{7}\over{2}}}}\over{7}}+{{6\,\left(x-1 \right)^{{{5}\over{2}}}}\over{5}}+2\,\left(x-1\right)^{{{3}\over{2}} }+2\,\sqrt{x-1})
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 26 Nov 2011, 10:39
par sad13 » 26 Nov 2011, 10:39
Tu ne trompes pas de rubrique car je ne pense pas qu'on fasse ça au lycée vu que le changement de variable en intégration n'est pas....
merci et bon courage?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités