Primitive du produit de deux fonctions

[Waax22951]

Bonjour,
Serai juste pour savoir s'il existe une formule pour obtenir la primitive du produit de deux fonctions ?
Car je ne trouve pas de résultats de ce type quand je le cherche sur internet.. De la même manière, existe-t-il une formule pour obtenir la primitive de:
-

-
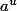
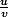
où u et v sont des fonctions et a un réel non nul.
Merci d'avance !

[capitaine nuggets]

Salut !

Bonjour,
Serai juste pour savoir s'il existe une formule pour obtenir la primitive du produit de deux fonctions ?
Car je ne trouve pas de résultats de ce type quand je le cherche sur internet.. De la même manière, existe-t-il une formule pour obtenir la primitive de:
-

-
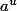
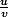
où u et v sont des fonctions et a un réel non nul.
Merci d'avance !

Pour la primitive de deux fonctions, tu peux voir du côté de "l'intégration par parties".

Que sont a,u et v ? Des fonctions ?

[Robic]

Il n'existe pas de formule pour la primitive d'un produit, d'un quotient, ou d'un a^u.

Par contre...

- Si on a un produit à primitiver, il faut regarder s'il ne peut pas s'écrire sous la forme u'u (ou u'u^n). Exemple : sin(x)cos(x) : c'est le produit d'une fonction et sa dérivée. Pareil avec ln(x)/x : c'est le produit de ln(x) par 1/x.

- Si on a un quotient à primitiver, il faut regarder s'il ne peut pas s'écrire sous la forme u'/u (ou u'/u^n). Exemple : 1/(x ln(x)) : c'est le quotient de 1/x par ln(x).

- Si on a un truc a^u, on l'écrit d'abord sous la forme exp(u ln(a)) où ln(a) joue le rôle d'une constante, donc c'est exp(v) où v = u ln(a). Dans ce cas, il faut regarder s'il ne s'écrit pas sous la forme v'exp(v). Exemple : x . 2^(x²) avec v = x² ln(2).

[Waax22951]

Je vois..
Et si la fonction est où est une constante réelle, qu'obtiendrait-on ? :hein:

[chan79]

Je vois..
Et si la fonction est où est une constante réelle, qu'obtiendrait-on ? :hein:

salut
avec x=3

on recherche a, b,c et d pour que soit une primitive de f
En dérivant,

En identifiant
a=-1
b=-3
c=-6
d=-6
les primitives de f sont



avec x non entier, faut voir, mais ça doit se compliquer

[Waax22951]

Justement, le problème de base portait justement sur les non entiers.. :ptdr:
Je n'ai pas trop compris l'explication:comment obtient-on ?
Merci pour vos réponse d'ailleurs :lol3:

[Robic]

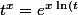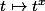
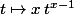
Si x n'est pas entier, ça ne change pas grand chose. En effet, en écrivant que tu peux démontrer que la dérivée de est , comme si x était un entier.

Quant à l'expression obtenue par Chan79, c'est tout simplement le résultat d'un calcul de dérivée assez long et ennuyeux qu'il n'a pas détaillé.

[chan79]

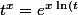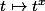
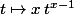
Si x n'est pas entier, ça ne change pas grand chose. En effet, en écrivant que tu peux démontrer que la dérivée de est , comme si x était un entier.

Quant à l'expression obtenue par Chan79, c'est tout simplement le résultat d'un calcul de dérivée assez long et ennuyeux qu'il n'a pas détaillé.

salut Robic
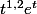
pour les primitives de , ça te ferait quoi ?

[Robic]

Ah, zut, c'est un peu plus compliqué en effet. En fait je réagissais par rapport au calcul de la dérivée, mais c'est vrai que pour l'écriture a priori de la primitive il vaut mieux avoir une puissance entière...

[Waax22951]

D'accord, je viens de comprendre.. ;)
On ne peut pas déterminer les primitives quand x est réel avec cette méthode, mais existe-t-il une autre façon de faire ? :hein: