Bonjour, j'aurai besoin de savoir si j'ai bien su faire cet exercice, merci d'avance :++: . Je vous donne l'énoncé :
Soit
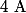
,
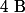
,
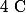
trois points de l'espace non-alignés de l'espace, et
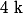
un réel.
On note

le barycentre des trois points pondérés
)
,
)
,
)
.
1°)a) Justifier l'existence de

pour tout réel
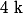
.
Pas très dur ^^.
b) Démontrer que :
pour tout réel
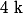
,

.
C'est fait.
c) Faire une figure et construire les points

,

et

.
Si

alors

.
Si

alors

, donc

.
Si

alors

.
Pour la figure, je l'ai faite.
2°) Soit

la fonction définie sur
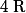
par :
= - \frac{x}{x^2+1})
a) Déterminer la limite de

en

et sa limite en

.

et

.
b) Etablir le tableau de variations de la fonction

sur
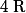
.
Pour le tableau de variations :
J'ai placé

et

et j'ai pris pour

les valeurs qui ont permis de placer les points

,

et

, c'est-à-dire,
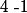
,
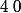
et
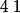
.
Ensuite, grace au calcul de la dérivée, j'ai établis que

est strictement positive sur

et sur

.
Donc

par de
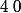
puis croit vers

puis décroit vers
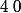
puis vers

pour enfin croitre à nouveau vers
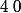
.
3°) En déduire l'ensemble des points

:
a) Lorsque
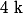
décrit l'intervalle

.
C'est le segment

b) Lorsque
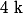
décrit l'intervalle

; on précisera le comportement du point

lorsque
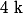
tend vers

.
C'est le segment

; lorsque
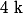
tend vers l'infini,

tend vers
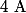
.
c) Lorsque
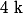
décrit l'intervalle

; on précisera le comportement du point

lorsque
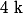
tend vers

.
C'est le segment

; lorsque
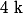
tend vers moins l'infini,

tend aussi vers
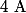
.
d) Lorsque
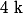
décrit
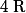
.
Ici, j'hésite, mais je dirai que c'est le segment

Merci encore d'avance pour votre aide :++: :king2:
