Pôlynome du second degré 1ère
21 messages
- Page 1 sur 2 - 1, 2
 Pôlynome du second degré 1ère
Pôlynome du second degré 1ère
Bonjour excusez-moi je dois déterminer un polynôme du second degré ayant pour racines -3 et 2 tel que P(0)=4... Je n'ai même pas pu commencer svp...
Modifié en dernier par Romuald380 le 05 Déc 2019, 15:01, modifié 1 fois.
Re: Déterminer un pôlynome du second degré ayant pour racine
Romuald380 a écrit:Je dois déterminer un polynôme du second degré ayant pour racines -3 et 2 tel que P(0)=4.
Tu n'as pas dans ton cours :
Un polynôme de degré 2 qui a pour racine x1 et x2 a pour forme factorisée a(x - x1)(x - x2)
?
Donc ton polynôme est P(x) = a(x + 3)(x - 2)
Et comme tu sais que P(0) = 4 ça te permet de déterminer a
Modifié en dernier par titine le 05 Déc 2019, 15:04, modifié 3 fois.
Re: Pôlynome du second degré 1ère
Romuald380 a écrit:On ne m'à jamais expliqué cette méthode
En quelle classe es tu ?
Qu'as tu vu sur les polynômes du second degré.
Re: Pôlynome du second degré 1ère
Je suis en classe de première. On ne m'avais jamais demandé auparavant de trouver un polynôme sachant ses racines. Dônc là je ne me retrouve pasJe suis en classe de première. On ne m'avais jamais demandé auparavant de trouver un polynôme sachant ses racines. Dônc là je ne me retrouve pas.
Re: Pôlynome du second degré 1ère
C'est bon merci beaucoup. Grâce à vous j'ai pu trouver le polynôme.. C'est -2/3x^2-2/3x+4
Re: Pôlynome du second degré 1ère
Je suis en classe de première. On ne m'avais jamais demandé auparavant de trouver un polynôme sachant ses racines. Dônc là je ne me retrouve pasJe suis en classe de première. On ne m'avais jamais demandé auparavant de trouver un polynôme sachant ses racines. Dônc là je ne me retrouve pas.
Tu n'as pas vu cette propriété :
Un polynôme de degré 2 qui a pour racine x1 et x2 a pour forme factorisée a(x - x1)(x - x2)
?
Re: Pôlynome du second degré 1ère
Si si j'ai vu cette propriété. C'est juste que je ne savais pas qu'on devait l'utiliser. Mais maintenant c'est bon j'ai tout compris. Merci
Re: Pôlynome du second degré 1ère
Romuald380 a écrit:C'est bon merci beaucoup. Grâce à vous j'ai pu trouver le polynôme.. C'est -2/3x^2-2/3x+4
Exact !
Re: Pôlynome du second degré 1ère
As-tu pensé à une méthode plus directe ?
=4) ,
, 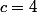
(2) = -6=\dfrac{c}{a}) ,
, 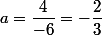
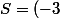 + (2)= -1 = -\dfrac{b}{a}) ,
, 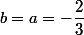
Modifié en dernier par Carpate le 05 Déc 2019, 16:10, modifié 1 fois.
Re: Pôlynome du second degré 1ère
C'est c'est bon j'ai tout compris. Merci pour la méthode j'enregistre déjà ça. Merci
Re: Pôlynome du second degré 1ère
Romuald380 a écrit:Je comprends un peu la méthode. Mais pas totalement.
on a l'expression des racines:
d'où en faisant la somme
en faisant le produit
et c=4
Modifié en dernier par mathelot le 05 Déc 2019, 16:03, modifié 1 fois.
Re: Pôlynome du second degré 1ère
mathelot a écrit:Romuald380 a écrit:Je comprends un peu la méthode. Mais pas totalement.
on a l'expression des racines:
d'où en faisant la somme
en faisant le produit
et c=4
J'ai compris merci.
J'essaie de déterminer un polynôme du second degré admettant 1 pour seule racine tel que P(0)=2... J'essaie avec cette méthode mais je ne trouve pas le polynôme.
Re: Pôlynome du second degré 1ère
Romuald380 a écrit:J'essaie de déterminer un polynôme du second degré admettant 1 pour seule racine tel que P(0)=2... J'essaie avec cette méthode mais je ne trouve pas le polynôme.
1 n'est pas la seule racine mais une racine double. Tu peux retrouver les formules en faisant x_1=x_2=1
Re: Pôlynome du second degré 1ère
mathelot a écrit:Romuald380 a écrit:J'essaie de déterminer un polynôme du second degré admettant 1 pour seule racine tel que P(0)=2... J'essaie avec cette méthode mais je ne trouve pas le polynôme.
1 n'est pas la seule racine mais une racine double. Tu peux retrouver les formules en faisant x_1=x_2=1
Ah oui ah oui. Je viens de trouver. J'ai trouvé comme polynôme -2 (x-1)^2 en utilisant cette méthode.
Re: Pôlynome du second degré 1ère
Romuald380 a écrit:mathelot a écrit:Romuald380 a écrit:J'essaie de déterminer un polynôme du second degré admettant 1 pour seule racine tel que P(0)=2... J'essaie avec cette méthode mais je ne trouve pas le polynôme.
1 n'est pas la seule racine mais une racine double. Tu peux retrouver les formules en faisant x_1=x_2=1
Ah oui ah oui. Je viens de trouver. J'ai trouvé comme polynôme -2 (x-1)^2 en utilisant cette méthode.
il y a une erreur de signe : a=2 et pas -2
Re: Pôlynome du second degré 1ère
Okay okay. Merci beaucoup pour la méthode. Bonne journée à vous...
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
