Point par rapport a une droite
16 messages
- Page 1 sur 1
 Point par rapport a une droite
Point par rapport a une droite
Bonjour,
je possède une liste de points dans un repère 2d avec leurs coordonnées et une droite d'équation de la forme y=ax+b. Comment je peut déterminer le point le "plus a gauche" formant un angle droit avec la droite ? et "le plus a droite".
Merci pour l'aide =)
je possède une liste de points dans un repère 2d avec leurs coordonnées et une droite d'équation de la forme y=ax+b. Comment je peut déterminer le point le "plus a gauche" formant un angle droit avec la droite ? et "le plus a droite".
Merci pour l'aide =)
Re: Point par rapport a une droite
Bonjour
Comment un point peut-il former un angle (droit ou pas) avec une droite?
Comment un point peut-il former un angle (droit ou pas) avec une droite?
Re: Point par rapport a une droite
Oui je me suis mal exprimé.
Par exemple on a un point A quelconque de ma liste et un point B qui se trouve la droite et tel que AB forme un angle droit avec la droite.
Je cherche donc les 2 points de la liste qui sont les plus aux extrémités par rapport à la droite et aux autres points de la liste.
Par exemple on a un point A quelconque de ma liste et un point B qui se trouve la droite et tel que AB forme un angle droit avec la droite.
Je cherche donc les 2 points de la liste qui sont les plus aux extrémités par rapport à la droite et aux autres points de la liste.
Re: Point par rapport a une droite
Le point B a pour coordonnées (xB,axB+b) puisqu'il est sur la droite.
La droite (AB) perpendiculaire à la droite a pour pente -1/a
Son équation est donc y-yA=(-1/a)(x-xA) comme B est aussi sur cette droite ses coordonnées vérifient cette équation, donc
axB+b-yA=(-1/a)(xB-xA)
équation qui donne xB.
Bien sûr il y a d'autres solutions (méthodes je voulais dire)...
La droite (AB) perpendiculaire à la droite a pour pente -1/a
Son équation est donc y-yA=(-1/a)(x-xA) comme B est aussi sur cette droite ses coordonnées vérifient cette équation, donc
axB+b-yA=(-1/a)(xB-xA)
équation qui donne xB.
Bien sûr il y a d'autres solutions (méthodes je voulais dire)...
Modifié en dernier par Tiruxa47 le 09 Mar 2017, 17:25, modifié 1 fois.
Re: Point par rapport a une droite
Si plusieurs points sont sur une droite, comment connait-on le point le "plus a gauche" et le point "le plus a droite" ?
Re: Point par rapport a une droite
Si la droite n'est pas parallèle à l'axe des ordonnées et que le vecteur unité de l'axe des abscisses est orienté de gauche à droite, alors l'abscisse la plus grande correspond au point le plus à droite et inversement.
Re: Point par rapport a une droite

Par exemple avec le polygone suivant
Comment trouve t-on le point le plus a droite ( ici C dans notre cas ) par rapport à la droite (ED) et le point le plus a gauche (ici A dans notre cas)
Re: Point par rapport a une droite
bonsoir
C le plus "a droite" par rapport a (ED) ?... s'il s'agit de la distance a la droite (ED), B est plus "a droite"
A "a gauche" de (ED) ? quelque soit la direction sur la droite (ED) qui permette de determiner la droite et la gauche , A et C sont du même coté!
pourrais-tu preciser ton probleme? en particulier la definition de la droite et de la gauche.......
comme on te l'a dit il faut:
ecrire l'equation de (ED)
ecrire l'equation de sa perpendiculaire passant par C
determiner les coordonnees de P intersection des deux droites
calculer la longueur |PC|
.......
recommencer avec les autres points et comparer
........ apres avoir defini la droite et la gauche!
C le plus "a droite" par rapport a (ED) ?... s'il s'agit de la distance a la droite (ED), B est plus "a droite"
A "a gauche" de (ED) ? quelque soit la direction sur la droite (ED) qui permette de determiner la droite et la gauche , A et C sont du même coté!
pourrais-tu preciser ton probleme? en particulier la definition de la droite et de la gauche.......
comme on te l'a dit il faut:
ecrire l'equation de (ED)
ecrire l'equation de sa perpendiculaire passant par C
determiner les coordonnees de P intersection des deux droites
calculer la longueur |PC|
.......
recommencer avec les autres points et comparer
........ apres avoir defini la droite et la gauche!
Modifié en dernier par siger le 09 Mar 2017, 18:00, modifié 1 fois.
Re: Point par rapport a une droite
Oui si on projecte perpendiculairement les points A, B, C sur la droite (ED), on voit que A et C seront aux éxtrémitées et B quelque part au milieu.
Re: Point par rapport a une droite
re
aux extremités de quoi?
tu parles de droite ou de segment?
j'avoue avoir du mal a comprendre......
il semble que tu parles de "droite" et de "gauche" par rapport aux extremites du segment donc par rapport a une droite perpendiculaire au segment?
aux extremités de quoi?
tu parles de droite ou de segment?
j'avoue avoir du mal a comprendre......
il semble que tu parles de "droite" et de "gauche" par rapport aux extremites du segment donc par rapport a une droite perpendiculaire au segment?
Re: Point par rapport a une droite
En gros je cherche a faire un rectangle qui va englober le polygone.
Donc pour cela je prend un coté au hasard du polygone -> ED
Ensuite il faut que je trouve de "combien" vers la gauche le rectangle doit aller pour englober le tout a "gauche", le côté gauche du rectangle passera donc par A
et de meme à droite le côté droit du rectangle passera par C.
Donc pour cela je prend un coté au hasard du polygone -> ED
Ensuite il faut que je trouve de "combien" vers la gauche le rectangle doit aller pour englober le tout a "gauche", le côté gauche du rectangle passera donc par A
et de meme à droite le côté droit du rectangle passera par C.
Re: Point par rapport a une droite
Le plus rapide il me semble est de calculer le produits scalaire 
Le résultat représente l'abscisse du point A' projeté orthogonal de A sur l'axe (ED) de repère (E, )
)
De même ensuite pour
Le résultat représente l'abscisse du point A' projeté orthogonal de A sur l'axe (ED) de repère (E,
De même ensuite pour
Re: Point par rapport a une droite
re
il me semble que le plus simple est de:
1- changer de reprere
utiliser un repere (E,ED,ED')
calculer les coordonnees de chaque point
retenir les points extremes en x<0 et x>0
retenir les points extremes en y<0 et y >0
tracer un rectangle basé sur ces points (cote parallele a (ED))
2- ecrire dans le repere actuel l'equation de (ED)
determiner les projections orthogonale de chaque point sur (ED) , en utilisant les perperdiculaires passant par chaque point ou en utilisant le produit scalaire
retenir les points d'anscisses extremes <0 ou >0
calculer la distance de chaque point a (ED)
retenir les points de plus grande distance
tracer un rectangle basé sur ces points (cote parallele a (ED))
il me semble que le plus simple est de:
1- changer de reprere
utiliser un repere (E,ED,ED')
calculer les coordonnees de chaque point
retenir les points extremes en x<0 et x>0
retenir les points extremes en y<0 et y >0
tracer un rectangle basé sur ces points (cote parallele a (ED))
2- ecrire dans le repere actuel l'equation de (ED)
determiner les projections orthogonale de chaque point sur (ED) , en utilisant les perperdiculaires passant par chaque point ou en utilisant le produit scalaire
retenir les points d'anscisses extremes <0 ou >0
calculer la distance de chaque point a (ED)
retenir les points de plus grande distance
tracer un rectangle basé sur ces points (cote parallele a (ED))
Re: Point par rapport a une droite
Salut,
Je suis pas sûr d'avoir compris la question, mais, si tu as l'équation d'une droite sous la forme
sous la forme 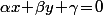 et un point
et un point ) alors la distance de
alors la distance de  à la droite
à la droite  (c'est à dire la distance de
(c'est à dire la distance de  à son projeté orthogonal) est donné par
à son projeté orthogonal) est donné par \!=\!\dfrac{|\alpha x_o\!+\!\beta y_o\!+\!\gamma|}{\sqrt{a^2+b^2}})
(et c'est très facile à démontrer en utilisant les produit scalaires)
De plus, le signe de te dit de quel coté de la droite le point
te dit de quel coté de la droite le point  est situé.
est situé.
Bref, si tes points ont pour coordonnées_{1\leq i\leq n}) , pour trouver "le plus à droite" et "le plus à gauche" (s'ils existent), il faut chercher parmi les
, pour trouver "le plus à droite" et "le plus à gauche" (s'ils existent), il faut chercher parmi les  lequel est le plus grand positif et lequel est le plus petit négatif (mais s'ils sont par exemple tous positifs, y'a pas de "plus petit négatif", mais c'est normal vu que tout les points sont du même coté de la droite).
lequel est le plus grand positif et lequel est le plus petit négatif (mais s'ils sont par exemple tous positifs, y'a pas de "plus petit négatif", mais c'est normal vu que tout les points sont du même coté de la droite).
Enfin, si ton équation "de départ" est sous la forme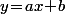 , il faut l'écrire par exemple
, il faut l'écrire par exemple  donc calculer les différents
donc calculer les différents  (et chercher le max. positif et le min. négatif)
(et chercher le max. positif et le min. négatif)
Je suis pas sûr d'avoir compris la question, mais, si tu as l'équation d'une droite
(et c'est très facile à démontrer en utilisant les produit scalaires)
De plus, le signe de
Bref, si tes points ont pour coordonnées
Enfin, si ton équation "de départ" est sous la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Point par rapport a une droite
Par contre y'a un truc que je pige pas dans ton laïus :Temporaire a écrit:
Comment trouve t-on le point le plus a droite ( ici C dans notre cas ) par rapport à la droite (ED) et le point le plus a gauche (ici A dans notre cas)
Si on parcours la droite (ED) de D vers E alors les points A , B , C sont tous "à droite" et, évidement, si on la parcours de E vers D, ils sont tous "à gauche".
Bref, A , B ,et C sont tout les trois du même coté de la droite (ED) et je comprend pas comment tu te "place" par rapport à la droite (ED) pour voir C "à droite" et A "à gauche" de la droite (ED) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Point par rapport a une droite
Ah, si, je vient (éventuellement) de comprendre : ce que tu regarde, ce n'est pas la position des points par rapport à la droite, mais la position sur la droite des projetés orthogonaux des points.
Dans ce cas, il faut que tu prenne les deux points qui donnent le minimum et le maximum des (
( si ta droite est donnée sous la forme
si ta droite est donnée sous la forme 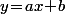
Dans ce cas, il faut que tu prenne les deux points qui donnent le minimum et le maximum des
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
