PGCD
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nythostyle
- Membre Relatif
- Messages: 113
- Enregistré le: 22 Juil 2018, 17:17
-
 par nythostyle » 18 Sep 2024, 18:53
par nythostyle » 18 Sep 2024, 18:53
Bonjour, je suis tombé sur une question qui m'a laissée un peu perplexe quant à comment attaquer le problème, j'ai la solution du problème que je posterai si demandé, mais je souhaite plutôt m'intéresser à comment initier la démarche de résolution :
Pour quels pairs d'entiers positifs la séquence suivante est elle toujours constante pour n = 1,2,....,
PGCD (

,

)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Sep 2024, 13:06
par Ben314 » 19 Sep 2024, 13:06
Salut,
Salut.
Si

(ou

) est nul, ça marche.
Sinon, la valeur constante doit être
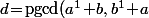\!=\!a\!+\!b)
et

doit diviser

et
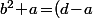^2\!+\!a)
c'est à dire

et

donc il doit diviser
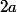
et,, comme

, cela signifie qu'on doit avoir

, c'est à dire
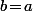
.
Enfin, pour que

soit constant, il faut que
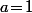
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
catamat
- Habitué(e)
- Messages: 1365
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 19 Sep 2024, 16:27
par catamat » 19 Sep 2024, 16:27
Bonjour
J'en étais au même point avec une petite variante :
a+d divise a²+b et a+b²
donc a+b divise a²+b-a-b² qui est égal à (a-b)(a+b-1)
comme a+b et a+b-1 sont premiers entre eux, a+b divise a-b
or a+b divise a+b donc a+b divise a-b+a+b=2a
-
nythostyle
- Membre Relatif
- Messages: 113
- Enregistré le: 22 Juil 2018, 17:17
-
 par nythostyle » 19 Sep 2024, 17:20
par nythostyle » 19 Sep 2024, 17:20
Merci beaucoup à vous, je trouve la démarche remarquablement claire et bien expliquée Ben merci à toi !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités