Petit Théorème de Fermat

[Neeb]

Bonjour à tous.

Je n'arrive pas à traiter une question d'arithmétique en rapport avec le petit théorème de FERMAT. Si quelqu'un peut m'aider ça serait sympa !

Voici l'énoncé.

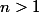
Pour tout , montrez que est divisible par 30.

Merci à ceux qui jeterons un coup d'oeil

[titine]

J'ai trouvé la solution suivante :

n^5 - n est divisible par 5 (petit théorème Fermat)

n^5 - n = n(n^4 - 1) = n(n² + 1)(n² - 1) = (n^3 + n)(n² - 1)
Or n^3 - n divisible par 3 (petit théorème Fermat) donc n^5 - n divisible par 3.

n^5 - n = n(n² + 1)(n² - 1) = n(n² + 1)(n + 1)(n - 1)
Or n(n + 1) divisible par 2 donc n^5 - n divisible par 2.

Conclusion : n^5 - n est divisible par 5, 3 et 2 donc il est divisible par 30.

Je suis sure qu'il y a beaucoup plus simple ... !

[Neeb]

Merci Titine !

[Daragon geoffrey]

bonjour titine, ton raisonnement est bon exepté une petite erreur (il me semble) quand tu affirmes que n^3 + n divisible par 3 d'aprè fermat, c'ne seré pas plutôt n^3 - n divisible par 3 selon le petit th de fermat ! enfin il fo que tu justifies que n^5 - n=(n^ 2 +1)(n-1)n(n+1) est divisible par 2 car (n-1), n et (n+1) sont 3 entiers consécutifs donc l'un d'entre eux o moin est pair donc divisible par 2 ! @ +

[titine]

Oui bien sûr !
Effectivement c'est n^3 - n qui est divisible par 3.
Et comme n^5 - n = n(n^4 - 1) = n(n² - 1)(n² + 1) = (n^3 - n)(n² +1) alors n^5 - n est divisible par 3.
Et évidemment, n(n+1) est divisible par 2 car n et n+1 sont des entiers consécutifs.
Bon, enfin, faut rédiger ça correctement ...

[flight]

salut,

le petit theoreme de fermat dit que (a^p)-a est divisible par p si p est premier

dans notre cas 5 est premier alors n^5-n est divisible par 5

on peut donc ecrire que n^5-n=5.q

en mutipliant par 6 les deux membres de cette équation , on peut ecrire que

6n^5-6n=30.q

en terme de modulo , on peut ecrire 6n^5=6.n[30]

et 6n^5/6=6n/6[30] soit n^5=n[30] (je sais pas si la manip est bonne !...)

alors n^5-n est divisible par 30

[Quidam]

6n^5/6=6n/6[30] soit n^5=n[30] (je sais pas si la manip est bonne !...)

Pour info, la manip n'est pas "bonne" ! Tu peux multiplier les deux membres de :
6n^5=6n [30]
par n'importe quel nombre ! Mais pas diviser ! Pour diviser, il faudrait multiplier par l'inverse de 6 : or 6 n'a pas d'inverse : c'est un diviseur de 0 puisque 6*5=0 [30] !

C'est juste pour toi que je dis ça. Car le problème est parfaitement résolu depuis hier à 17 H 13 par titine, même si elle avait fait une petite faute de frappe que tout le monde avait corrigée...