Bonjour! :)
je m'en remet a vous comme dernier recours:
Depuis ce matin un probleme me travaille je n'arrive absolument pas a le résoudre si vous pouvez m'aider je vous en serez extremement reconnaissante
Un champ rectangulaire a un périmetre de 2km exactement, démontrez que son aire ne peut pas dépasser 25 hectares....
alors jai mis tout ça en systeme avec équations et inéquations mais je n'arrive pas a les résoudre! je planche dessus depuis hier soir...
Un petit probleme complexe^^
7 messages
- Page 1 sur 1
par bernie » 04 Déc 2005, 15:43
Bonjour,
soit x la longueur et y la largeur :
x+y=1000( en mètres : OK) Cette somme doit rester constante. On va montrer que le produit est au plus de 250 000 (en m² car 25ha=250000m²).
Dans l'équa du second degré :
ax²+bx+c=0 (1), on a 2 racines :
x1=(-b+V(b²-4ac))/2 et x²=(-b-V(b²-4ac))/2)-->V=racine carrée.
Tu montres que x1+x2=S=-b/a et x1*x2=P=c/a
(1) peut s'écrire en divisant par"a" :
x²+(b/a)x+c/a=0
soit x²-Sx+P=0
Cette équation n'a de racine que si :
S²-4P>=0 soit 4P<=S² soit P<=S²/4
Donc la valeur maxi de P est S²/4 : OK?
Dans ton pb valeur maxi de P=1000²/4=250000
A+
soit x la longueur et y la largeur :
x+y=1000( en mètres : OK) Cette somme doit rester constante. On va montrer que le produit est au plus de 250 000 (en m² car 25ha=250000m²).
Dans l'équa du second degré :
ax²+bx+c=0 (1), on a 2 racines :
x1=(-b+V(b²-4ac))/2 et x²=(-b-V(b²-4ac))/2)-->V=racine carrée.
Tu montres que x1+x2=S=-b/a et x1*x2=P=c/a
(1) peut s'écrire en divisant par"a" :
x²+(b/a)x+c/a=0
soit x²-Sx+P=0
Cette équation n'a de racine que si :
S²-4P>=0 soit 4P<=S² soit P<=S²/4
Donc la valeur maxi de P est S²/4 : OK?
Dans ton pb valeur maxi de P=1000²/4=250000
A+
par bernie » 04 Déc 2005, 15:45
J'ai écrit :
x1=(-b+V(b²-4ac))/2 et x²=(-b-V(b²-4ac))/2)-->V=racine carrée.
C'est : x1=(-b+V(b²-4ac))/2 et x2=(-b-V(b²-4ac))/2)
Et comprends que x1 et x2 sont les dimensions du rectangle. Vois bien la suite.
x1=(-b+V(b²-4ac))/2 et x²=(-b-V(b²-4ac))/2)-->V=racine carrée.
C'est : x1=(-b+V(b²-4ac))/2 et x2=(-b-V(b²-4ac))/2)
Et comprends que x1 et x2 sont les dimensions du rectangle. Vois bien la suite.
par becirj » 04 Déc 2005, 15:45
Bonjour
En appelant x et y les deux dimensions, on a S= x+y =1 km =10 hm.
Deux nombres qui ont pour somme S et pour produit P sont solutions de l'équation du second degré :
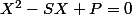
Cette équation admet des solutions si son discriminant est supérieur ou égal à 0 soit
P=xy donc on obtient que l'aire xy a pour valeur maximale 25 hm^2=25 ha
En appelant x et y les deux dimensions, on a S= x+y =1 km =10 hm.
Deux nombres qui ont pour somme S et pour produit P sont solutions de l'équation du second degré :
Cette équation admet des solutions si son discriminant est supérieur ou égal à 0 soit
P=xy donc on obtient que l'aire xy a pour valeur maximale 25 hm^2=25 ha
par bernie » 04 Déc 2005, 15:49
Dernière précision :
cela revient à dire que , comme P est max pour S²-4P=0, c'est que les 2 racines sont une racine double donc que ton rectangle est en fait un carré.
A périmètre constant pour un rectangle, la plus grande aire est obtenue avec un carré.
Retiens ça aussi.
cela revient à dire que , comme P est max pour S²-4P=0, c'est que les 2 racines sont une racine double donc que ton rectangle est en fait un carré.
A périmètre constant pour un rectangle, la plus grande aire est obtenue avec un carré.
Retiens ça aussi.
par bernie » 04 Déc 2005, 16:17
Olivia qui est prudente a posé ce pb sur un autre site et je lui ai donné la réponse pour une élève de seconde. Tu vas voir Olivia ce que tu en penses?
A+
A+
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :