Bon si on commence au début soit en deux dimensions
Deux droites si elles sont sécantes se coupent en un point, ok c'est pas nouveau...
Si on utilise les équations paramétriques
Droite (AB)
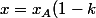+ k x_B)
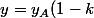+ k y_B)
Droite (CD)
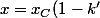+ k' x_D)
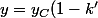+ k' y_D)
L'éventuel point commun s'obtient en résolvant le système suivant d'inconnue (k,k')
+ k x_B=x_C (1-k')+ k' x_D)
+ k y_B=y_C (1-k')+ k' y_D)
ou
+ k'(x_C-x_D)=x_C - x_A)
+ k'(y_C-y_D)=y_C - y_A)
On a une solution unique si et seulement si le déterminant de ce système est non nul donc si et seulement si

et
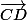
ne sont pas colinéaires.
Si on passe en dimension 3 on va avoir 4 paramètres pour 3 équations seulement donc dans le cas où les plans sont sécants les 4 paramètres vont s'exprimer en fonction d'un seul paramètre et on obtient une équation de droite.
Enfin en dimension 4 on a 6 paramètres et 4 équations donc si les conditions sont réunies( hyperplans sécants), ces 6 paramètres vont s'exprimer en fonction de deux paramètres et on a une équation de plan.
