Bonjour à tous et à toutes.
J'ai des petits questions sur la parité de fonction^^
Une fonction est-elle forcément paire et/ou impaire ou peut elle être ni l'un ni l'autre.
De plus, si la dérivée d'une fonction est paire. la fonction est impaire?
et si la fonction dérivée est impaire. La fonction est elle paire?
Peu on aussi parler de Suite paire et impaire?
Merci infiniment pour vos réponses^^
Parité d'une fonction
6 messages
- Page 1 sur 1
Re: Parité d'une fonction
Salut, par définition une fonction f est paire (resp. impaire) si quel que soit x dans le domaine  de f, son opposé -x appartient à
de f, son opposé -x appartient à  et f(-x)=f(x) (resp. f(-x)=-f(x).
et f(-x)=f(x) (resp. f(-x)=-f(x).
Donc déjà ça dépend du domaine : s'il n'est pas symétrique par rapport à 0, c'est foutu (par exemple, la fonction racine carré). Après, tu peux par exemple choisir une fonction affine, c'est-à-dire de la forme f(x)=ax+b, avec a non nul. En revanche, on a un résultat qui dit que toute fonction définies sur peut s'exprimer de manière unique comme somme d'une fonction paire et d'une fonction impaire. Par exemple, tu as
peut s'exprimer de manière unique comme somme d'une fonction paire et d'une fonction impaire. Par exemple, tu as 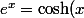+\sinh(x)) .
.
Quelle est la dérivée de la fonction) ?
?
Quelle est la dérivée de la fonction) ?
?
Sachant que si deux fonctions sont égales, leur dérivée l'est aussi, déduis-en que :
- si f(-x)=f(x) alors f'(-x)=-f'(x),
- si f(-x)=-f(x) alors f'(-x)=f'(x).
Et tu peux ainsi répondre à ta question
Une suite n'est ni plus ni moins qu'une fonction dont le domaine est intersecté avec . Donc inutile de parler de parité pour une suite puisque son domaine ne sera jamais symétrique par rapport à 0.
. Donc inutile de parler de parité pour une suite puisque son domaine ne sera jamais symétrique par rapport à 0.
Donc déjà ça dépend du domaine : s'il n'est pas symétrique par rapport à 0, c'est foutu (par exemple, la fonction racine carré). Après, tu peux par exemple choisir une fonction affine, c'est-à-dire de la forme f(x)=ax+b, avec a non nul. En revanche, on a un résultat qui dit que toute fonction définies sur
Quelle est la dérivée de la fonction
Quelle est la dérivée de la fonction
Sachant que si deux fonctions sont égales, leur dérivée l'est aussi, déduis-en que :
- si f(-x)=f(x) alors f'(-x)=-f'(x),
- si f(-x)=-f(x) alors f'(-x)=f'(x).
Et tu peux ainsi répondre à ta question
Une suite n'est ni plus ni moins qu'une fonction dont le domaine est intersecté avec
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Parité d'une fonction
Si f(x) = x²
f(-x) = (-x)² = x² = f(x) donc f est une fonction paire.
Dérivée f'(x)= 2x
f'(-x) = 2(-x) = -2x = -f'(x) donc fonction dérivée impaire !
Maintenant, une dérivée paire ou impaire n'implique pas une parité sur la fonction.
Exemple f(x)= 3x+ 2
Fonction ni paire, ni impaire, mais dérivée paire.
f(-x) = (-x)² = x² = f(x) donc f est une fonction paire.
Dérivée f'(x)= 2x
f'(-x) = 2(-x) = -2x = -f'(x) donc fonction dérivée impaire !
Maintenant, une dérivée paire ou impaire n'implique pas une parité sur la fonction.
Exemple f(x)= 3x+ 2
Fonction ni paire, ni impaire, mais dérivée paire.
Re: Parité d'une fonction
tomtom a écrit:Une fonction est-elle forcément paire et/ou impaire ou peut elle être ni l'un ni l'autre.
une fonction f peut être ni paire ni impaire
exemple: f(x)=x+2
tomtom a écrit:si la dérivée d'une fonction est paire. la fonction est impaire?
pas nécessairement, par exemple:
f(x)=x^3+1
f'(x)=3x^2
par contre, si f' est continue sur R et paire, la primitive F de f' qui s'annule en x=0
est impaire.
on pose u=-t
tomtom a écrit: si la fonction dérivée est impaire. La fonction est elle paire?
on pose u=-t
Si f' est continue et impaire, ses primitives sont paires (la constante d'intégration est une fonction paire)
Re: Parité d'une fonction
Super Merci Mathelot merci nodgim
Cela me parait clair maintenant
Merci beaucoup à tous
Cela me parait clair maintenant
Merci beaucoup à tous

6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
