Bonjour,
J'ai besoin d'aide pour démontrer que 7/ n((n^6)-1).
j'ai passé un bon moment à essayer sans succès , j'ai essayé la récurrence et j'ai aussi ( en vain ) essayé les cas ( n=7k .... jusqu'à n=7k+6 ). Merci d'avance.
( Vos avis sont les bienvenus même vous n'avez pas de réponse )
Nouvelle question ( arithmétique )
6 messages
- Page 1 sur 1
aymane399 a écrit:Bonjour,
J'ai besoin d'aide pour démontrer que 7/ n((n^6)-1).
j'ai passé un bon moment à essayer sans succès , j'ai essayé la récurrence et j'ai aussi ( en vain ) essayé les cas ( n=7k .... jusqu'à n=7k+6 ). Merci d'avance.
( Vos avis sont les bienvenus même vous n'avez pas de réponse )
Par récurrence, ça doit pouvoir se faire. Mais le mieux ici est d'utiliser les congruences (ce qui revient à faire les disjonctions de cas que tu as proposé
Le cas
Ensuite, pour
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Tout d'abord je te remercie beaucoup ^^ , et puis la méthode du modulo j'ai pu démonter pour n=7k n=7k+1 et n=7k+6 le reste c'est pénible , j'ai réessayé la récurrence et j'y suis allé jusqu'au bout et ca a marché , c'est intimidant ( n+1)^6 mais bon il doit forcément y'avoir une solution plus simple.
aymane399 a écrit:Tout d'abord je te remercie beaucoup ^^ , et puis la méthode du modulo j'ai pu démonter pour n=7k n=7k+1 et n=7k+6 le reste c'est pénible
Si tu utilises les modulo, non :we:
Prenons le cas
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
As-tu vu les congruences ?
Si non, on peux le faire à ta manière si tu veux.
Si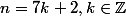 , trouve deux entiers
, trouve deux entiers  et
et  tels que
tels que 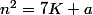 et
et 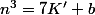 ,
,  (même si tu ne connais pas le développement de
(même si tu ne connais pas le développement de ^3) , tu dois pouvoir le retrouver sachant que
, tu dois pouvoir le retrouver sachant que ^3=(A+B)(A+B)^2)) .
.
Déduis-en un entier tel que
tel que 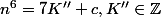 :+++:
:+++:
Si non, on peux le faire à ta manière si tu veux.
Si
Déduis-en un entier
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
